Riqueza de especies arbóreas en bosques de montaña de Chiapas: estimaciones a partir de datos de herbarios e inventarios florísticos
Elizabeth Campos-Sánchez(a), Mario González-Espinosa(a) ⁎ ✉ , Neptalí Ramírez-Marcial(a), Darío Alejandro Navarrete-Gutiérrez(b), Miguel Ángel Pérez-Farrera(c)
Resumen
La riqueza de especies arbóreas ( S ) frecuentemente ha sido estimada con inventarios sistemáticos. De manera reciente, la disponibilidad en línea de datos de herbario ha permitido otras aproximaciones. ¿Qué tan comparables son estas estimaciones de S ? Ajustamos modelos lineales generalizados (GLM) a estimaciones con ambos tipos de datos en 3 regiones montañosas de Chiapas (altitud > 1,500 m), relativamente bien conocidas desde una perspectiva florística y para las cuales se dispone de un significativo número de parcelas de inventarios. Se detectó con ambos tipos de datos un total de 792 especies arbóreas. El modelo de Clench estimó con datos de herbarios un total de 862 especies y 425 con inventarios. Los modelos GLM elegidos con los 2 tipos de datos mostraron una correlación positiva de S en 2 de las regiones, pero no en aquella con mayor riqueza. Los inventarios brindan una instantánea de la equidad entre especies en muestras reales de comunidades y representan un acervo útil para entender la estructuración de la diversidad. Los datos de herbario muestran que en la estructura de la diversidad obtenida con inventarios aún pueden estar presentes numerosas especies raras o de distribución restringida. Parece conveniente usar ambos tipos de datos de manera complementaria para evaluar la S en bosques tropicales, en especial cuando son pobremente conocidos.
© 2017 Universidad Nacional Autónoma de México, Instituto de Biología. Este es un artículo Open Access bajo la licencia CC BY-NC-ND
(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Palabras clave:
Bosques montanos; Bosques tropicales; Diversidad arbórea; Especímenes botánicos; Inventarios forestales; Modelos lineales generalizados;
Tree species richness in tropical montane forests of Chiapas: estimates from herbaria data and floristic surveys
Abstract
Estimates of tree species richness (S ) have usually been approached with systematic surveys. More recently, with the increasing on-line availability of digital herbaria data, alternative S estimates are possible. How comparable are these two estimates? We fitted generalized linear models (GLM) to obtain estimates of S with both data types from three different mountain regions in Chiapas (>1,500 elevation) for which substantial numbers of both herbarium vouchers and survey plots are available. A total number of 792 tree species were detected with both types of data. Clench’s model estimated 862 and 425 tree species with herbarium and survey data, respectively. The selected GLM models rendered S estimates that were positively correlated in two out of the three studied regions (not in the most species-rich region). Systematic surveys provide a snap-shot of species equitability among real samples of forest communities, and therefore, represent a useful set of data to approach the understanding of tree diversity structure. On the other hand, herbarium vouchers allow estimates of how many rare or restricted species may still be absent in the survey-based inventory. It seems convenient to make complementary use of both types of data in order to estimate S in poorly known tropical forests.
Keywords:
Montane forests; Tropical forests; Tree diversity; Herbarium vouchers; Forest surveys; Generalized linear models;
Introducción
La riqueza de especies de árboles determina los patrones de diversidad de especies de plantas y animales y sus funciones en los bosques tropicales ( Janzen, 1970; Novotny et al., 2006 ). Por ende, su estimación adecuada es esencial para establecer las necesidades y priorizar las acciones para la conservación y el manejo sustentable de los ecosistemas forestales ( Hubbell et al., 2008 ). Recientemente, se ha suscitado el interés por proponer estimaciones del número de especies de árboles en los bosques tropicales con un doble fin: 1) establecer una línea de base para dar seguimiento a la variación de la riqueza de especies en función de cambios de ámbitos regional o global provocados por las actividades humanas ( Hubbell et al., 2008; Slik et al., 2015; Ter-Steege et al., 2013 ) y, a la vez, 2) profundizar en la naturaleza de los datos y su interacción con los métodos de estimación (por ejemplo, Cayuela, Gotelli y Colwell, 2015 ). De manera general, se recurre al uso de 2 tipos de datos sobre la riqueza de especies de árboles tropicales: los obtenidos de las etiquetas de los especímenes depositados en herbarios y aquellos obtenidos mediante inventarios florísticos (o más a menudo con fines de manejo forestal; Baraloto et al., 2013; Cayuela et al., 2012 ). Sin embargo, las estimaciones disponibles con frecuencia no discuten las implicaciones que pueden derivarse del uso de uno u otro tipo de datos. La tabla 1 resume las principales ventajas y limitaciones inherentes a estos 2 tipos de información.
Ventajas y desventajas del uso de datos de especímenes de herbario e inventarios para la estimación de la riqueza de especies arbóreas.
| Herbarios a | Inventarios b | |
|---|---|---|
| Ventajas | Proveen una línea de base del conocimiento botánico en áreas geográficas determinadas | Revelan propiedades emergentes de las comunidades (diversidad, rareza, estructura, equidad, etc.) |
| Ahorran costos mediante el acceso electrónico a gran cantidad de información disponible mundialmente | Estiman S con algoritmos que proveen una aproximación al problema de los levantamientos aún incompletos | |
| Brindan certidumbre taxonómica, en especial si los especímenes son revisados periódicamente por especialistas | Identifican cambios temporales locales en la estructura y composición de las especies | |
| Ofrecen registros disponibles para escalas temporales y espaciales amplias | Comparan información sobre escalas amplias si los muestreos se efectúan de manera similar a lo largo del espacio y el tiempo. Definen de manera precisa el tamaño mínimo utilizado para incluir «especies arbóreas» (5 o 10 cm de dap [aprox. 130 cm]) |
|
| Desventajas | Introducen sesgos temporales, taxonómicos y geográficos propios del recolector de cada subconjunto de los datos disponibles | Cubren a menudo una menor área que la cubierta por los recolectores botánicos |
| Pueden incluir errores de nomenclatura persistentes por un periodo prolongado. Pueden carecer de detalles en la información geográfica de las localidades. Pueden omitir la recolección de un número variable de especies presentes en una localidad dada. Pueden incurrir en errores de inclusión de «especies arbóreas» para cuyos especímenes los recolectores pueden no brindar suficiente información sobre el diámetro, la altura y el hábito. Pueden subestimar la riqueza local cuando se obtiene mediante la sobreposición de los polígonos de las «áreas de distribución» derivadas de los especímenes disponibles |
Impiden comparaciones directas entre proyectos independientes por carencia de un protocolo estandarizado. Pueden diferir en los sistemas o procesos para la identificación de especies. Pueden representar con frecuencia altos niveles de esfuerzo y costo |
La riqueza de especies (S ) es un concepto abstracto, cuya estimación está casi siempre ligada al número de taxones específicos o subespecíficos encontrados por unidad de área (densidad de especies) o al número de individuos muestreados ( Gotelli y Colwell, 2001; Peet, 1974 ). La evaluación de S se ha abordado tradicionalmente con base en inventarios florísticos o forestales sistemáticos, en los cuales se asume que este atributo es espacial y temporalmente comparable ( Gotelli y Colwell, 2001 ). En el caso de las plantas, se han implementado distintos métodos para inferir patrones emergentes de las comunidades a partir solo de datos sobre la presencia de las especies (incidencia de las especies) o provenientes de la recolección de especímenes depositados en museos o herbarios, que incluso pueden haberse recolectado hace décadas —o inclusive— siglos ( Dorazio, Gotelli y Ellison, 2010; Pyke y Ehrlich, 2010; Garcillán y Ezcurra, 2011; Schmidt, Kreft, Thiombiano y Zizka, 2005; Zaniewski, Lehmann y Overton, 2002 ). Los métodos para inferir S a partir de este tipo de datos se pueden dividir en 2: los que modelan la distribución potencial de cada especie por separado (modelación de nichos) para luego sobreponer las distribuciones y obtener una estimación de S en un área determinada (Araújo y Guisan, 2006 ) y los que modelan la riqueza acumulada de los registros ( Benito, Cayuela y Albuquerque, 2013; Cayuela et al., 2009; Chapman y Purse, 2011; Elith et al., 2006 ). Aunque la estimación de S basada en la sobreposición de las distribuciones de los organismos es bastante promisoria, aún existen ciertas restricciones sobre el tipo de datos que esta familia de modelos puede incluir. Por ejemplo, para utilizar información de herbario en estos modelos se ha propuesto que se requieren al menos de 20 a 50 especímenes de la misma especie para modelar su distribución con menor incertidumbre ( Feeley y Silman, 2011 ). Esta cifra —que parece bastante modesta— está muy lejos de la realidad para la vegetación de muchas localidades tropicales: se ha calculado que el 38% de las especies de plantas de las áreas tropicales de Sudamérica, África y el sureste de Asia están representadas únicamente por un registro o espécimen; la media es de 2 y solo para el 2.3% de las especies se dispone de más de 20 registros ( Feeley y Silman, 2011 ). Esto quiere decir que 9 de cada 10 especies de plantas tropicales en el mundo están pobremente recolectadas y son «esencialmente invisibles para las herramientas de modelación y conservación» ( Feeley y Silman, 2011).
El presente trabajo estima la variación espacial de la riqueza de especies arbóreas en distintos tipos de bosques de montaña del estado de Chiapas a partir de la modelación con 2 fuentes de información complementarias: la proveniente de recolecciones taxonómicas depositadas históricamente en herbarios nacionales y del extranjero, y la disponible a partir de datos de inventarios de la flora leñosa obtenidos en distintas localidades ( www.biotreenet.com, Cayuela et al., 2012 ). Cabe aclarar que el objetivo de este trabajo no consiste en entender las causas de la variación de la riqueza de especies de la región de estudio, sino que solo se plantea evaluar qué tan discrepantes pueden resultar las estimaciones de S en función del conjunto de datos usados por los modelos. Por lo anterior, la hipótesis es que se espera encontrar: 1) un esfuerzo de muestreo diferenciado geográficamente entre inventarios y recolectas de especímenes, con algunas áreas mejor evaluadas que otras y 2) que el conjunto de datos de especímenes botánicos resultará en valores más altos de S debido a la más frecuente incorporación de especies raras o escasas. Con los resultados se pretende conocer el esfuerzo de muestreo (recolección de especímenes o inventarios) efectuado en las regiones de estudio y comparar la similitud o diferencia de las estimaciones que resultan de ambos tipos de datos e identificar cuáles podrían incentivarse para optimizar los esfuerzos de conocimiento botánico y conservación de la riqueza de especies de árboles en las regiones de estudio.
Materiales y métodos
Mediante un modelo digital de elevaciones ( Inegi, 2013 ) se identificaron las áreas del estado de Chiapas ubicadas por arriba de 1,500 m de altitud, cota altitudinal que se ha considerado útil para diferenciar la vegetación montana respecto a la tropical lluviosa ( González-Espinosa y Ramírez-Marcial, 2013 ); además, en estas áreas coincide la existencia de datos provenientes de especímenes de herbario y de datos de inventarios florísticos o forestales. Se delimitaron 3 polígonos que corresponden a las Montañas del norte, Los Altos de Chiapas y la Reserva de la Biosfera El Triunfo (REBITRI). Las áreas elegidas se encuentran dentro de las regiones fisiográficas definidas por Müllerried (1957) denominadas: sistema de las Montañas del norte, región de la Meseta Central y la Sierra Madre de Chiapas, respectivamente ( fig. 1 ). Los polígonos incluyeron un número variable de celdas de 10 km2 de extensión cada una. Las capas de información obtenidas fueron estandarizadas con una proyección de coordenadas métricas para la zona 15 con el DatumWGS 84 y divididas en 617 cuadros o celdas de 10 km2 en el programa QGis (Quantum GIS, 2009).
Ubicación de los polígonos estudiados en 3 regiones de Chiapas y la ubicación de Chiapas respecto al resto de México: a) Montañas del norte, b) Los Altos, c) la REBITRI. Se muestra la distribución espacial de las localidades donde se recolectaron los especímenes de herbario de las especies arbóreas (puntos negros) y la ubicación de los inventarios (círculos blancos) utilizados en el estudio.
El estado de Chiapas se ubica en la parte más sureña de México y limita con Guatemala, Oaxaca, Veracruz, Tabasco y el océano Pacífico ( fig. 1 ). Las Montañas del norte de Chiapas son un conjunto de serranías geológicamente complejas. En cuanto a los tipos de vegetación, resalta en las partes altas y húmedas el bosque mesófilo de montaña (BMM) y en las partes bajas los bosques de pino-encino, pino-encino-liquidambar y bosques estacionales perenifolios y subperenifolios ( Breedlove, 1981).
Al sureste se encuentra la región conocida como Los Altos de Chiapas, la cual ocupa aproximadamente 11,000 km2 . Esta región muestra el predominio de climas templados y templados-fríos ( García, 1987 ). Se ha documentado que existen en ambas regiones alrededor de 300 especies de árboles que pueden ser componentes del BMM ( González-Espinosa y Ramírez-Marcial, 2013; González-Espinosa, Meave, Lorea-Hernández, Ibarra-Manrríquez y Newton, 2011 ). La vegetación de ambas regiones ha sido afectada de forma severa por las actividades humanas y originalmente incluía asociaciones de bosques de encino, bosques de pino-encino y BMM ( Breedlove, 1981; González-Espinosa y Ramírez-Marcial, 2013; Miranda, 1952 ).
Por su parte, la REBITRI posee una superficie de 1,192 km2 ( Arreola-Muñoz, Cuevas-García, Becerril-Macal, Noble-Camargo y Altamirano, 2004; Cortina-Villar et al., 2012 ) y se inserta dentro de los límites del norte de la región del Soconusco. Presenta un gradiente altitudinal desde los 460 hasta los 2,500 m, lo que da lugar a que se presenten al menos 4 tipos de clima, que van desde el cálido húmedo hasta el templado húmedo ( García, 1987 ). Debido a esta amplia heterogeneidad ambiental, diversas clasificaciones como las de Miranda y Hernández (1963), Rzedowski (1978), Breedlove (1981) y Pérez-Farrera (2004) , entre otras, han reconocido entre 10 y 11 tipos de vegetación. Destaca por su extensión y riqueza florística el BMM. Actualmente cuenta con 5 zonas núcleo decretadas en 1990 ( Cortina-Villar et al., 2012 ). Aunque en la región se ha realizado una extensa exploración y recolección botánica, es comparativamente menor la existencia de inventarios florísticos.
Se recopiló una base de datos con información de especímenes de especies arbóreas resguardadas en los herbarios MEXU, CAS, DS, XAL, ECOSUR, CHIP y MO ( Holmgren, 1990 ). La información fue obtenida de 3 fuentes: la base de datos recopilada por el grupo académico de conservación y restauración de bosques de El Colegio de la Frontera Sur (ECOSUR), la cual consiste en un compendio de especímenes de especies arbóreas recolectados en Chiapas durante los 150 años previos a 2000 ( González-Espinosa, Rey-Benayas, Ramírez-Marcial, Huston y Golicher, 2004 ); la información disponible en línea de The Global Biodiversity Information Facility (GBIF, 2013 ) y la base de datos del herbario Eizi Matuda de la Universidad de Ciencias y Artes de Chiapas, correspondientes a especímenes árboreos recolectados en la Sierra Madre de Chiapas (Martínez-Camilo, Pérez-Farrera y Martínez-Meléndez, 2012; Martínez-Meléndez, Pérez-Farrera y Farrera-Sarmiento, 2008; Pérez-Farrera y Gómez-Domínguez, 2010; Pérez-Farrera, Martínez-Camilo, Martínez-Meléndez, Farrera-Sarmiento y Maza-Villalobos, 2012 ). Se realizó una estandarización de la nomenclatura botánica con ayuda de la rutina Taxonstand (Cayuela et al., 2012 ), que identifica errores ortográficos y sinonimias en el ambiente de programación R ( R Core Team, 2013 ), al establecer una conexión con The Plant List ( www.theplantlist.org ), base taxonómica de plantas vasculares auspiciada por los Royal Botanic Gardens (Reino Unido) y el Missouri Botanical Garden (EUA). Posteriormente, se eliminaron los registros repetidos. Solo se utilizaron registros de especies arbóreas (individuos monopódicos, con diámetro a la altura del pecho [130 cm], dap≥5cm y altura≥4m; González-Espinosa y Ramírez-Marcial, 2013; González-Espinosa et al., 2004, 2011; Grandtner, 2005; Parker, 2008 ) y aquellos que contaban con referencias geográficas explícitas o bien que pudieran ubicarse espacialmente con la información de las etiquetas. En total se utilizaron 7,431 registros ( fig. 1 ) de especímenes que corresponden a 740 especies arbóreas.
Se utilizó la información de inventarios disponibles en línea en el proyecto BIOTREE (http://www.biotreenet.com/espanol/html/ ), una red de inventarios forestales del sur de México y Centroamérica ( Cayuela et al., 2012 ). Para los polígonos de interés, se incluyeron 395 inventarios que, en conjunto, evaluaron a más de 40,000 individuos (dap ≥5 cm) correspondientes a 367 especies arbóreas (fig. 1).
Se realizó una recopilación del número total de familias, géneros y especies encontrados por conjunto de datos y polígonos de estudio. Además, los datos se ajustaron a un modelo no lineal o curva de acumulación de especies por conjunto total de datos realizada con el programa EstimateS ( Colwell, 1997) y con el uso de R (R Core Team, 2013 ). Los especímenes se asociaron a las celdas realizadas para cada polígono. Para elegir las celdas informativas (CI), o suficientemente bien recolectadas, solo se utilizaron celdas con más de 40 registros ( González-Espinosa et al., 2004 ). En cada una, se calculó una curva de recolección de especímenes, utilizando este número como medida indirecta del esfuerzo de muestreo ( Soberón y Llorente, 1993 ). Las curvas resultantes fueron ajustadas al modelo exponencial de Clench con un método de iteración quasi-Newton. Después, se calculó el número de registros necesarios para una tasa de incremento de una especie por cada 100 nuevos registros ( Hortal y Lobo, 2002 ). De este modo, se eligieron las celdas que poseían igual o mayor número de registros estimados con la fórmula anterior. Estos análisis fueron realizados con los programas EstimateS 9.10 ( Colwell, 1997) y Statistica (StatSoft, 1998).
Para elegir las CI con los datos de inventarios, solo se utilizaron las celdas que contenían parcelas que evaluaron las comunidades forestales con parcelas de 1,000 m 2 . Para cada celda se construyeron curvas de acumulación con las abundancias de cada especie. Las curvas se ajustaron al modelo de Clench para comparar los resultados obtenidos con base en los especímenes disponibles en herbarios. Para elegir las CI se calculó el número de individuos por celda para representar el 80% de la S total y se eligieron las celdas que contenían este o un mayor número de individuos, con base en la recomendación de Jiménez-Valverde y Hortal (2003) .
Se utilizaron diferentes estimaciones de S con cada conjunto de datos para la estimación de la riqueza de especies. Con el conjunto de datos de herbario, se encontró que algunas de las estimaciones de S con la función de Clench (S Clench ) tienden a sobrestimar la riqueza; por ello, se decidió utilizar para la modelación la S observada (S obs ) por celda. En el caso de los inventarios, se decidió utilizar la S est con el modelo de Clench.
Se obtuvieron las variables climáticas y topográficas reproyectadas para México ( tabla 2; Cuervo-Robayo et al., 2013; Inegi, 2013 ). Cada capa fue proyectada y muestreada para la resolución del análisis con el método de interpolación bilineal. Se extrajeron los valores por celda con la estandarización de los datos a valores de media igual a cero y varianza igual a uno. La latitud y longitud fueron estandarizadas al restar el valor de la media a cada caso ( Hortal y Lobo, 2002 ). Solo se utilizaron variables climáticas y topográficas ( tabla 2 ). Se calcularon 3 variables adicionales: la evapotranspiración real anual (ETR A ) y la de las épocas seca (ETRS) y húmeda (ETRH ) con la fórmula de Turc (1954, «fide» González-Espinosa et al., 2004 ).
Variables geográficas, topográficas y climáticas utilizadas para generar los modelos ambientales.
| Variables geográficas | |
| LAT | Latitud |
| LONG | Longitud |
| Variables topográficas | |
| Altmax | Altitud máxima (m) |
| Alt_med | Altitud media (m) |
| Alt_min | Altitud mínima (m) |
| Altrng | Intervalo de altitud (m) |
| Pend | Exposición de la pendiente (grados) |
| Variables climáticas | |
| ETRA | Evapotranspiración real anual (mm) |
| ETRS | Evapotranspiración real de la época seca (mm) |
| ETRH | Evapotranspiración real de la época húmeda (mm) |
| ETRTASA | Tasa estacional de evapotranspiración |
| b1 | Temperatura media anual (°C) |
| b2 | Amplitud media diurna (media mensual [temperatura máx-temperatura min]) |
| b3 | Isotermalidad (b2/b7)(100) |
| b4 | Estacionalidad de la temperatura (coeficiente de variación) |
| b5 | Temperatura máxima del mes más cálido (°C) |
| b6 | Temperatura mínima del mes más frío (°C) |
| b7 | Amplitud de temperatura anual (b5-b6) (°C) |
| b8 | Temperatura media del trimestre más húmedo (°C) |
| b9 | Temperatura media del trimestre más seco (°C) |
| b10 | Temperatura media del trimestre más caliente (°C) |
| b11 | Temperatura media del trimestre más frío (°C) |
| b12 | Precipitación anual (mm) |
| b13 | Precipitación del mes más lluvioso (mm) |
| b14 | Precipitación del mes más seco (mm) |
| b15 | Estacionalidad de la precipitación (coeficiente de variación) |
| b16 | Precipitación del trimestre más húmedo (mm) |
| b17 | Precipitación del trimestre más seco (mm) |
| b18 | Precipitación del trimestre más caliente (mm) |
| b19 | Precipitación del trimestre más frío (mm) |
Se ajustaron modelos lineales generalizados con una distribución de errores gamma y una función «link» logarítmica ( Cayuela, Rey-Benayas, Justel y Salas-Rey, 2006; Guisan y Edwards, 2002; Hortal y Lobo, 2002 ), uno para cada tipo de dato. Previamente, se realizó una matriz de correlaciones de las variables predictivas. En cada caso — debido a que la intención de modelar S en este estudio no fue encontrar una relación causal entre las variables predictivas y las explicativas, sino maximizar el ajuste sin considerar la colinearidad de las variables — , se evitó utilizar variables altamente correlacionadas ( r ≥ 0.8, Cayuela, Rey-Benayas, Justel y Salas-Rey, 2006 ). Se incorporó en el modelo cada variable y sus funciones cuadrática y cúbica de manera independiente. Se construyó el modelo, primero, con las variables que más explicaban la Sy que no estuvieran altamente correlacionadas. Después, se eliminaron de los modelos las variables que tuvieran menos influencia en la devianza total del modelo (selección por pasos hacia atrás, «backwards»). Cuando todas las variables fueron significativas, se añadió el polinomio de 9 términos de las variables espaciales (latitud y longitud; «trend surface analysis», según Hortal y Lobo, 2002 ) para aminorar la autocorrelación espacial. Estos 9 términos fueron posteriormente sometidos a una selección de pasos hacia atrás hasta que todos los parámetros resultantes fueran significativos.
De cada modelo resultante se analizaron los residuos para identificar valores extremos o «outliers». Para los modelos candidatos, se realizó en R con la rutina «ape» ( Hortal y Lobo, 2002; Cayuela et al., 2006 ) una prueba de autocorrelación de la I de Moran sobre los residuos y categorías de distancia geográfica similares a la longitud de las unidades territoriales. Después se realizaron mapas de pronóstico para verificar si el modelo resultaba en datos coherentes en la extrapolación. Con los modelos generados se siguió un procedimiento de validación cruzada. Con ello se estimó el porcentaje de error absoluto de cada modelo con la fórmula 1/n∑(y−yˆ)y×100 ( Cayuela et al., 2006) donde y es la S obs y yˆ es la S est de cada modelo. El inverso de este número corresponde al poder predictivo del modelo y con base en él y en el criterio de información de Akaike se eligieron los modelos con mayor poder explicativo ( Hortal y Lobo, 2002 ). Para evaluar qué tan congruente era la información resultante de cada modelo, se realizó la correlación entre las Sestimadas en cada celda por ambos modelos para ver las afinidades y discrepancias de los modelos a nivel regional. Al final, se realizó un mapa con el promedio de las celdas de ambos modelos.
Resultados
De las 617 celdas incluidas en este estudio, 104 corresponden al polígono de las Montañas de norte, 361 al de Los Altos de Chiapas y 152 al de la REBITRI. Al sobreponer los puntos de especímenes de herbario e inventarios en el total de celdas que componen los 3 polígonos de estudio ( fig. 1 ), se observó que los exploradores botánicos han visitado al menos una vez el 62.1% de las celdas evaluadas, mientras que los inventarios disponibles solo se encuentran en el 16.5% de las celdas. Los especímenes más antiguos registrados y utilizados en este estudio datan de mediados del siglo xx , mientras que los inventarios más antiguos son de 1995. Aun con estas diferencias espaciales y temporales de los individuos recolectados o inventariados, los grupos que han realizado los inventarios han incluido más de 40,000 registros de presencia de las especies de árboles, en comparación con los 7,431 especímenes recolectados incluidos en la base de datos ( tabla 3 ). Cuando se conjuntan ambas fuentes de información para obtener un listado general de especies arbóreas, la riqueza total o diversidad regional incluye 792 especies, de las cuales 740 se encuentran en el listado de especímenes de herbario (93.4%), mientras que los inventarios han reconocido únicamente 367 (46.3%), entre las cuales, sin embargo, se aportan 52 especies nuevas (6%) al total recopilado con ambos conjuntos de datos ( tabla 3 ). Cabe aclarar que el hecho de que estas 52 especies no se encuentren dentro del conjunto de datos de especímenes taxonómicos no implica que no se hayan recolectado en otras partes del estado ( González-Espinosa y Ramírez-Marcial, 2013 ).
Número de registros y las familias, géneros y especies que se encuentran representados en los 2 conjuntos de datos de cada región.
| Especímenes de herbario | Especímenes | Familias | Géneros | Especies | |
|---|---|---|---|---|---|
| Montañas del Norte | 1,065 | 73 | 153 | 266 | |
| Los Altos de Chiapas | 4,522 | 82 | 233 | 478 | |
| REBITRI | 1,844 | 87 | 236 | 483 | |
| Total | 7,431 | 98 | 312 | 740 | |
| Inventarios | Registros | Familias | Géneros | Especímenes de herbario | |
| Montañas del Norte | 4,069 | 49 | 73 | 116 | |
| Los Altos de Chiapas | 29, 938 | 65 | 133 | 209 | |
| REBITRI | 7, 584 | 64 | 132 | 210 | |
| Total | 41,591 | 78 | 198 | 367 | |
| Total | 98 | 331 | 792 |
En ambos conjuntos de datos, a nivel de región, Los Altos de Chiapas resultó ser el área más extensa y más ampliamente recolectada o inventariada, seguida de la REBITRI y de las Montañas del norte. El número de familias, géneros y especies encontradas en las Montañas del norte fue el menor con ambos tipos de datos. El área con mayor riqueza de familias y géneros fue la REBITRI, tanto a partir de especímenes de herbarios como con información de inventarios. La riqueza de especies encontrada en la REBITRI y en Los Altos fue notablemente similar, independientemente de las diferencias en la extensión del área de ambas regiones y del tipo de datos que la documentan. Con ambas aproximaciones se encontró una diferencia de solo 5 especies (478 vs. 483 con el caso de especímenes) y 1 especie (209 vs. 210 en el caso de los inventarios) ( tabla 3).
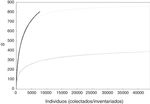
A nivel de especies, al modelar una curva de acumulación total para cada conjunto de datos se encontró que el número de especies estimado con los datos de inventarios se acumuló mucho más lentamente que cuando se utilizaron los especímenes de herbario. Con las curvas ajustadas por el modelo de Clench se estimó con el conjunto de datos de herbario el doble de especies esperadas que el correspondiente para los inventarios ( fig. 2).
Curvas de acumulación suavizadas obtenidas con bases de datos de especímenes de herbario (negro) e inventarios (gris). Las líneas punteadas representan el ajuste del modelo de Clench con información de inventarios ( Sn =0.17n/1+[0.0004n], N =41,591, a/b = 425) y especímenes de herbarios ( Sn =0.69n/1+[0.0008n], N =7,431, a/b =862.2). Véase Soberón y Llorente (1993) para detalles y bases teóricas de la derivación del modelo de Clench.
Con el conjunto de datos de especímenes de herbario se encontraron 27 celdas que se pudieron considerar como bien muestreadas, con las que se eligió el modelo de S con base en el criterio de información de Akaike (AIC). El modelo que presentó el valor más bajo de AIC fue:
S obs = exp{4.45 (−0.41ETR TASA )+(−0.85b2)+(0.68b13)+(−0.33Alt rng )+(0.33[b6 + b6 2])+(0.27Alt max )+(−0.5ETR S )+(0.4b7)}
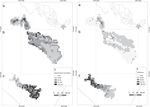
Este modelo explicó el 85.5% de la devianza, con un poder predictivo de 89.8% y un AIC final de 227 ( tabla 4). La I de Moran (I = −0.052) mostró que las clases de distancia geográfica con la estructura de los residuos no están espacialmente correlacionadas ( p =0.83). El mapa de la figura 3 se obtuvo al extrapolar el modelo a las 617 celdas que componen los polígonos de estudio, el cual predice una mayor riqueza de especies al sureste de la REBITRI, al noroeste de la región de Los Altos de Chiapas y al norte de la región de las Montañas del norte. Las variables incorporadas que se relacionaron con la temperatura fueron la amplitud media diurna (− b2 ), la amplitud media anual de temperatura (+ b7 ) y la ecuación cuadrática de la temperatura del mes más frío (+ b6 ), en orden de aportación al modelo. En cuanto a variables relacionadas con la precipitación, se obtuvo que la precipitación del mes más lluvioso (+ b13 ) fue la que tuvo mayor aportación a la ecuación final. También se integraron la tasa de evapotranspiración real (− ETR TASA ) y la evapotranspiración real del mes más seco (− ETR S ). Finalmente, la altitud máxima ( Alt max ) y el intervalo de altitud (− Alt rng ) fueron las variables con menor poder explicativo en la regresión final ( tabla 4).
Ajuste de modelos de variables ambientales para explicar S obs con los datos de especímenes de herbarios.
| Variable | Devianza | F | gl | D 2 | p | AIC | Signo |
|---|---|---|---|---|---|---|---|
| Modelo nulo | 3.016 | 27 | 266.47 | ||||
| Tasa de evapotranspiración estacional | 2.64 | 17.4 | 26 | 12.29 | 0.0005 | 264.68 | − |
| Amplitud media diurna (mensual T max -T min) | 2.00 | 29.5 | 25 | 33.55 | 0.00003 | 258.84 | − |
| Precipitación del mes más lluvioso | 1.49 | 23.6 | 24 | 50.49 | 0.0001 | 252.52 | + |
| Intervalo de altitud | 1.38 | 5 | 23 | 54.15 | 0.0376 | 252.4 | − |
| Temperatura mínima del mes más frío | 1.08 | 13.9 | 22 | 64.31 | 0.0014 | 247.49 | − |
| Altitud máxima | 0.95 | 6 | 21 | 0.68 | 0.025 | 245.93 | + |
| Evapotranspiración de la época seca | 0.78 | 8 | 20 | 74.13 | 0.0107 | 242.31 | − |
| Amplitud de temperatura anual | 0.43 | 16.2 | 19 | 85.54 | 0.0007 | 227.65 | + |
Predicción de la distribución espacial de la riqueza de especies en celdas de 10 km2 estimada con datos de especímenes de herbarios (izquierda) o de inventarios (derecha) en 3 regiones de Chiapas (México): a) Montañas del norte, b) Los Altos, c) REBITRI.
Para este conjunto de datos, se encontraron 28 celdas bien muestreadas con las que el ajuste final del modelo elegido fue:
S Clench = exp{4.072+(−0.51[b2 + b2 2])+(7.172b17)+(−7.05ETR S )+(0.32Alt max )+(2.282e-10 XY)
Al omitir 2 datos extremos (N = 26), el modelo explicó el 86.1% de la devianza, tuvo un poder predictivo de 79.4% y un AIC final de 204.2. No se encontró evidencia de autocorrelación espacial ( I =−0.06, p =0.74). Este modelo tuvo menos términos que el obtenido con los datos de herbarios; 3 de ellos coincidieron con el anterior en cuanto a sus signos, aunque en este caso el término cuadrático de la amplitud media diurna de temperatura ( b2 2 ) resultó con mayor poder explicativo que la variable a la primera potencia. En el modelo obtenido con datos de inventarios, la variable relacionada con la precipitación que se incorporó fue la del trimestre más seco ( b17 ) y se añadió el término de interacción entre la longitud ( X) y latitud (Y) por resultar significativa (tabla 5 ). Al extrapolar este modelo en el mapa ( fig. 3 ), se registró mayor riqueza en la parte noreste de la REBITRI. En cuanto a los otros 2 polígonos estudiados, el modelo obtenido con datos de inventarios predijo una mayor riqueza en el noroeste, tanto de Los Altos de Chiapas como de las Montañas del norte.
Ajuste de variables ambientales para explicar la S obtenida del modelo S Clench con los datos de inventarios.
| Variable | Devianza | F | gl | D 2 | p | AIC | Signo |
|---|---|---|---|---|---|---|---|
| Modelo nulo | 7.23 | 25 | 244 | ||||
| Amplitud media diurna (mensual T max -Tmin ) | 3.58 | 65.4 | 24 | 50.48 | <0.0000 | 227.54 | − |
| Precipitación del trimestre más seco | 2.35 | 21.94 | 23 | 67.5 | 0.00014 | 218.43 | + |
| Evapotranspiración de la época seca | 2.12 | 4.03 | 22 | 70.7 | 0.053 | 212.78 | − |
| Altitud máxima | 1.64 | 8.68 | 21 | 77.31 | 0.007 | 212.97 | + |
| Latitud×longitud | 1.08 | 9.9 | 20 | 85.06 | 0.005 | 204.19 | + |
AIC: criterio de información de Akaike; D 2 : devianza residual; gl: grados de libertad.
Al correlacionar el valor de S de las celdas que resultaron de ambos modelos, se obtuvo una relación muy baja, pero significativa ( r =0.18, p <0.001, N = 617). Los valores estimados por el modelo derivado de datos de inventarios fueron, en promedio, menores a las estimaciones con los datos de herbarios. En 2 de las 3 regiones estudiadas, se encontró una relación positiva de la riqueza de especies estimada a partir de ambos conjuntos de datos, con r ≥ 0.5. Al contrario, en la región de la REBITRI se observó una r =−0.38 (fig. 4 ). Finalmente, al promediar los valores de S obtenidos en cada celda con ambos modelos, se obtuvo un mapa con valores más conservadores ( fig. 5 ). Resalta la mayor riqueza local promedio de la REBITRI respecto a las otras 2 regiones estudiadas.
Predicción de la distribución espacial de la riqueza de especies en celdas de 10 km2 en 3 regiones de Chiapas (México) con base en el promedio de 2 modelos, uno basado en especímenes de herbario y el otro derivado de datos de parcelas de inventarios. a) Montañas del norte, b) Los Altos, c) REBITRI.
Discusión
A primera vista, la pregunta parece sencilla ¿cuántas especies arbóreas puede haber en las regiones montañosas de Chiapas? Solo con base en las estimaciones de las curvas de acumulación de las especies calculadas con los datos de inventarios ecológicos, la respuesta hubiera sido: alrededor de 400. Al utilizar los especímenes de recolectas botánicas, este número se duplica. Las 792 especies arbóreas recopiladas con base en ambos conjuntos de datos disponibles en los polígonos de estudio —que en su conjunto son la diversidad regional o gamma conocida— representan el 52.2% de las 1,516 especies arbóreas conocidas para los 17 tipos de vegetación con dominancia de árboles en Chiapas ( González-Espinosa y Ramírez-Marcial, 2013 ). A su vez, dicha riqueza corresponde al 19.8% de las 4,044 especies de árboles estimadas para todo el país por Villaseñor y Ortiz (2013).
Aun cuando los árboles tienen una importancia ecológica como componentes estructurales de los ecosistemas que influyen sobre la diversidad local ( Laurance et al., 2006; Novotny et al., 2006; Pereira et al., 2010; Slik et al., 2015 ), la realidad es que aún no se pueden realizar estimaciones certeras sobre su riqueza en regiones megadiversas ( Gentry, 1992; Slik et al., 2015 ) y, menos aún, si los métodos de obtención de la información son muy diferentes. Recientemente, se publicó un cálculo de cuántas especies de árboles tropicales hay en el mundo, con base en la extrapolación de las amplitudes de abundancias de las especies obtenidas con inventarios, con lo que se llega a una estimación de entre 43,000 y 53,000 especies, de las cuales solo se observaron 11,371 ( Slik et al., 2015 ). Específicamente, para la región neotropical se estiman entre 18,000 y 23,000, de las cuales en los inventarios se encuentran solo cerca de 4,000 ( Slik et al., 2015 ). Esto tiene al menos 2 consecuencias importantes: que hay una gran laguna en el conocimiento respecto a la riqueza e identidad de las especies de árboles tropicales y que, si estas cifras fueran ciertas, hay una proporción de al menos un tercio de la diversidad con especies muy raras y con poblaciones muy pequeñas ( Hubbell, 2015; Ter-Steege et al., 2013 ) que no son ni han sido incluidas en los inventarios ecológicos. Con base en los resultados del presente trabajo, y aún si se considera que en los herbarios se encuentra depositada solo una parte de lo que es la riqueza de especies real, resalta que para estimaciones de tipo regional el uso de información asociada a especímenes taxonómicos es claramente útil. De hecho, con el nivel de conocimiento de la riqueza florística que se tiene en la actualidad, cualquier estimación que no los incorpore carecería de un importante aporte de información. Es un hecho que los estimadores del número de especies, calculados con base en curvas de acumulación, pueden aproximarnos a cuántas especies nos faltan por muestrear, pero no cuáles ( Gotelli, 2004 ). Normalmente, se considera que son las especies raras las que estarían en necesidad de una mayor prioridad de atención para su conservación, dado que son las especies con mayores riesgos de extinción en el BMM de México ( González-Espinosa et al., 2011 ). En este estudio se confirma que estas especies escasas no alcanzan a ser incluidas en muestreos ni en inventarios sistemáticos con el nivel de extensión y detalle de los que se han realizado a la fecha. En el análisis de los patrones de diversidad enfocados a especies raras, los conjuntos de información derivada de los herbarios pueden ser más útiles, prácticos y confiables que los inventarios ecológicos o forestales. Con el fin de obtener listas regionales —en este estado incipiente del conocimiento acerca de la diversidad — los acervos museológicos representarían, sobre cualquier otro medio, lo más cercano a reconocer la riqueza regional e identidad de las especies ( Gotelli, 2004).
Las curvas de acumulación de los conjuntos totales de especies obtenidas en el presente estudio permiten ver cómo con los especímenes de herbario la adición de especies nuevas es mucho más rápida al compararla con el conjunto de datos de inventario. ¿Por qué los inventarios efectuados en las regiones de estudio, habiendo evaluado 6 veces el número de individuos que los recolectores botánicos incorporaron a los herbarios, fallan en encontrar la riqueza que estos últimos encuentran? Se ha propuesto que si basamos nuestras estimaciones de la diversidad de especies en las comunidades, en datos de herbarios se obtienen visiones distorsionadas debido a una inadecuada información sobre su estructura ( Funk y Richardson, 2002; Rich y Woodruff, 1992). Ello se debe a que en estos acervos las especies raras están sobrerrepresentadas respecto a las especies comunes y más abundantes ( Funk y Richardson, 2002; Garcillán y Ezcurra, 2011; Guralnick y van-Cleve, 2005; Rich y Woodruff, 1992; Ter-Steege, Haripersaud, Banki y Schieving, 2011 ). Este patrón no aleatorizado de la distribución espacial de las especies de árboles es especialmente importante en organismos de hábitos sésiles; de ahí la importancia de la aleatoriedad de los muestreos para la evaluación de su diversidad ( Gotelli, 2004; Magnussen, 2011 ) y de la elección de los estimadores de riqueza. Por lo anterior, la mayoría de los índices relacionados con la diversidad requieren de una estimación de «la importancia» de cada especie —dada por su abundancia— para poder caracterizar de una manera más objetiva a una comunidad ( Peet, 1974).
Los inventarios sistemáticos son necesarios para caracterizar una comunidad a nivel ecológico y acercarnos a dilucidar los patrones y procesos que influyen en la distribución, persistencia y abundancia de las especies. A cuenta de lo anterior, en un estudio en la selva amazónica se calculó una riqueza estimada de alrededor de 16,000 especies de árboles, y se reconoció una hiperdominancia por únicamente 227 especies; esto significa que el 1.4% de las especies son las más comunes y se propone que, al incluir entre ellas más del 50% del total de los árboles individuales en la Amazonia, son responsables de la mayor parte de las funciones ecosistémicas en esa macrorregión ( Ter-Steege et al., 2013).
En este estudio se pretendió aminorar el sesgo de la representatividad de los datos de herbario y de inventarios con el uso solo de la información de las celdas «bien recolectadas» ( Hortal, Lobo y Jiménez-Valverde, 2007; Lobo, 2008; Lobo, Castro y Moreno, 2001 ). Esta elección nos priva de una cantidad de información existente de herbarios e inventarios que, si bien no es útil para un análisis adecuado, nos permite ajustar modelos predictivos de una manera más conservadora y sólida.
Con respecto a los modelos presentados en este estudio, es preciso hacer una distinción entre los modelos ecológicos explicativos, cuyo objetivo es entender la contribución de las variables determinantes de los parámetros bajo estudio —en este caso la riqueza de especies— , y los modelos predictivos, que están enfocados a explicar estadísticamente una variable, dada una serie de datos. Los últimos pueden no tener hipótesis previas y están encaminados a buscar modelos sencillos para maximizar el ajuste de los datos a las variables ambientales de diversa índole que se evalúan ( González-Espinosa et al., 2004; Guisan y Edwards, 2002; Lobo et al., 2001 ). Es común que los modelos de este tipo no puedan extrapolarse fuera del área del estudio en la que se realiza. En el presente análisis no se encontró un consenso para el área de la REBITRI, ya que cada modelo predice una mayor acumulación de la riqueza de especies de árboles en sitios opuestos. Ante la posibilidad de que los errores pueden concentrarse en las áreas del espectro geográfico y ambiental que han sido muestreados con menor intensidad ( Hortal et al., 2007 ), el área menos inventariada o recolectada entre las consideradas en este estudio fue la de las Montañas del norte. En el área de la REBITRI muchos de los trabajos realizados se han centrado en el llamado polígono i debido a su accesibilidad (Long y Heath, 1991 ), aunque ya desde hace más de 60 años Matuda, así como Miranda y Hernández obtuvieron especímenes de herbario en el cerro Ovando ( Breedlove, 1981 ), y recientemente se han publicado inventarios florísticos de áreas dentro de los polígonos iii y iv ( Martínez-Camilo et al., 2012; Martínez-Meléndez et al., 2008; Pérez-Farrera y Gómez-Domínguez, 2010; Pérez-Farrera et al., 2012 ). Lo anterior y la amplia heterogeneidad y riqueza arbórea del sitio — donde se ha estimado una densidad arbórea de más de 1,900 individuos por hectárea ( Gómez-Velasco et al., 2004)— pueden haber provocado estas discrepancias.
Estos modelos predictivos tampoco pretenden dar una explicación causal de la riqueza de especies asociada a variables ambientales. Sin embargo, estudios que sí han estado encaminados a entender los procesos indican que algunas de las variables predictivas que resultaron significativas en los modelos están relacionadas con la riqueza de especies, tales como la altitud ( Lobo et al., 2001 ), la evapotranspiración ( Alba-López, González-Espinosa, Ramírez-Marcial y Castillo-Santiago, 2003; González-Espinosa et al., 2004 ), así como otros atributos climáticos relacionados con la dinámica de la precipitación y la disponibilidad de la energía (O’Brien, 2000 ). Esta riqueza es consecuencia directa de la interacción de factores bióticos y físicos dados por la heterogeneidad e historia geológica, que se traducen en una alta variedad de formaciones forestales en el estado ( Breedlove, 1981; González-Espinosa, Ramírez-Marcial, Méndez-Dewar, Galindo-Jaimes y Golicher, 2005 ). La instantánea de la riqueza de especies de árboles obtenida en este estudio también tiene que ver —en menor medida — con el nivel de esfuerzo de muestreo dado por la recopilación de cada tipo de datos en cada área considerada. La región más rica en especies arbóreas que se señala con ambos tipos de datos es la REBITRI, la cual no es ni la más extensa ni la más ampliamente explorada. En su conjunto, las regiones de estudio son lugares con una alta riqueza arbórea en términos relativos para sistemas con climas templados ( Breedlove, 1981 ) y presentan una alta diversidad regional asociada a valores de diversidad alfa o S local de magnitud variable. Al respecto, ambos modelos indicaron valores estimados de magnitud parecida, aunque no en la misma proporción, ya que con los datos de herbario se reconocen más celdas con mayor riqueza. Para este tipo de comparaciones sería deseable ajustar un tercer modelo en el que se conjunten los datos de inventario a manera de incidencias junto con los de colectas para obtener otro conjunto de CI y ajustar la S obs con otras variables (Hortal y Lobo, 2002 ), que por razones de tiempo disponible no se realizó en este estudio. Sin embargo, en el mapa de los promedios de ambos modelos ajustados ( fig. 5 ), aunque se reportan menores valores de riqueza, se identifican más áreas con más especies y se alcanza un mayor consenso.
La modelación de la riqueza de especies con base en los especímenes depositados en herbarios muestra ventajas para su aplicación en regiones de alta diversidad, particularmente cuando las especies han sido poco recolectadas, y puede complementar la información sobre la distribución potencial para los taxones mejor conocidos. Los datos de herbario permiten acercarse a la composición y estructura de las comunidades al incluir especies raras, mientras que la información derivada de inventarios representa una «instantánea» de la equidad o dominancia de las especies en comunidades reales y permite acercarse a aspectos funcionales de la diversidad. Las 2 fuentes de información resultaron en estimaciones ampliamente discrepantes en cada una de las 3 áreas estudiadas, no obstante el considerable esfuerzo previo para su recopilación. El desarrollo de estimadores de S con ambas fuentes de información podría traducirse en valores más realistas sobre la riqueza de especies arbóreas y su distribución. El presente trabajo contrasta la complejidad del uso de ambos conjuntos de datos y apunta a la necesidad de contar con mejores estimaciones de la riqueza que resulten más fáciles de interpretar por quienes toman decisiones. Esta información es esencial para la implementación de políticas de aprovechamiento forestal y de conservación que incluyan el análisis de la pérdida de cobertura arbórea, los procesos de degradación en la composición de especies y el manejo y uso de los bosques por la población. Las discrepancias detectadas en este estudio dejan ver la necesidad de definir y exigir de manera explícita el origen de la información usada en las estimaciones de riqueza de especies de árboles en estudios de impacto ambiental, así como en los planes de manejo de áreas naturales protegidas y de unidades de aprovechamiento. Por ende, esta definición debiera incorporarse en los documentos normativos para la aplicación de políticas públicas sobre conservación y desarrollo y valorarse la conveniencia de aprovechar ambos tipos de información.
Agradecimientos
Agradecemos a Rubén Martínez Camilo por aportar información original a la base de datos y a Sandra Chediack, M. L. Martínez Vázquez y a un revisor anónimo por sus valiosos comentarios. ECS agradece al Consejo Nacional de Ciencia y Tecnología (Conacyt) por otorgar una beca para estudios de posgrado (núm. CVU. 501587) que hicieron posible el proyecto. Financiado con recursos fiscales 2012-2014 asignados a MGE y a ECS a través de la Dirección de Posgrado de ECOSUR.
Referencias
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.