A single genealogical lineage from the Sonoran Desert and the Mexican Pacific Coast explains the haplotype distribution of Trichobaris compacta

Un solo linaje del Desierto Sonorense y de la costa del Pacífico mexicano explica la distribución de haplotipos de Trichobaris compacta

The Mexican transition zone is the area in which the Neotropical and Nearctic biotas overlap (Halffter, 1976). In a strict sense, this zone includes the highlands of Mexico and Guatemala, whereas northern Mexico and southern United States are clearly Nearctic, and the lowlands of southern Mexico and Central America are clearly Neotropical (Morrone, 2015). Few assemblages of interactions among insects and their host plants have been documented in this Nearctic-Neotropical transition zone, even though their study offers a unique opportunity to link coevolving interactions with different evolutionary affinities.

The interaction between Trichobaris (Curculionidae) and their host plants (Solanum L. and Datura L.) occurs in this diverse and complex Nearctic-Neotropical transition zone. The weevils of the genus Trichobaris have a Nearctic distribution whereas South America is the ancestral area of origin of the Solanaceae family (Dupin et al., 2016), and the region in central Mexico is the area with the greatest species richness of Datura and is thought to be the diversification center (Luna-Cavazos & Bye, 2011).

From the 12 species of Trichobaris, only Trichobaris compacta (Casey, 1892) uses several Datura species as a food. Weevils oviposit into immature fruit, and then larvae eat developing seeds and associated tissues, whereas adults eat leaf tissue. Adults of Trichobaris compacta mate and rest on the host plant (Barber, 1935 and personal observations). Some studies show that this species is unable to develop in other solanaceous species, such as Nicotiana spp. (Diezel et al., 2011). Thus, this weevil is restricted to the Datura plant species. Trichobaris compacta occurs from southeastern USA to northern and central Mexico (Barber, 1935). The geographic distribution of T. compacta (Barber, 1935) differs from that of Datura species that uses as host plants. Datura wrightii is distributed in the deserts of USA and Mexico (Sonoran Desert), whereas D. discolor inhabits the Mexican Pacific Coast and Balsas basin. Datura inoxia occurs in the highlands in central Mexico and USA (Chihuahuan Desert), whereas D. reburra and D. pruinosa are only present in small areas in Mexico (northwest Mexico: states of Sinaloa and Sonora; southern Mexico: states of Morelos, Guerrero and Oaxaca, respectively) (Luna-Cavazos & Bye, 2011). Barber (1935) noted that T. compacta uses several host plant species distributed across a wide geographic area thus possibly promoting the formation of “races” or genetically distinctive populations associated with a particular plant species. However, we have not found evidence of lineages associated to a particular host plant species of Datura (De la Mora et al., 2018).

Here, we aim to elucidate how the genetic variation of Trichobaris compacta is geographically distributed. To this end, we analyzed a fragment of COI gene in individuals from different populations. This genetic marker has been used to test the presence of major genetic discontinuities causing population structure, most likely due to extrinsic barriers (Avise, 2004). Here, we show the (1) genetic diversity of 29 populations of T. compacta, population differentiation and structure estimates, (2) haplotype network, (3) the phylogeny of T. compacta haplotypes, and (4) historical demography.

Materials and methods

Trichobaris compacta occurs in southwestern USA (Barber, 1935) where it feeds upon Datura species. We collected Trichobaris compacta in populations of Datura plants along the Pacific coast of Mexico. For this study, T. compacta was collected on D. wrightii, D. inoxia, D. pruinosa, D. reburra and D. discolor. We selected localities in order to cover the entire distribution of T. compacta (based on Barber, 1935). Collected adult weevils were preserved in absolute alcohol for posterior analysis. Several fruits per plant were collected. To avoid sampling relatives inside a given fruit, we performed genetic analysis on only 1 weevil from each fruit. A total of 29 locations were sampled along the host plant distribution (Table 1; Fig. 1).

Each insect was frozen in liquid nitrogen (-196 °C), then macerated in an eppendorf tube using a micropestle. Genomic DNA was extracted using the DNeasy Tissue Kit (QiagenTM) according to the manufacturer’s protocol for animal tissue. We then amplified a 663-bp nucleotide protein coding region of the mitochondrial gene cytochrome c oxidase I (COI) by polymerase chain reaction (PCR), using the following primers: COA3107 (5´-TCT ATT ARD GGD GAD GCD CTA TCT TG-3´) and COS2183N (5´-CAR CAY YTA TTY TGR TTY TGR TTY TTY GG-3´) (Sota et al., 2004).

Each PCR (total volume of 25.5 ml) contained 1 ml of DNA (20 nM), 1 ml of each primer (10 mM), 0.2 ml of Taq polymerase (1U of Go Taq (Promega), 5 ml of Buffer 5x, 0.5 ml of each nucleotide (10 mM), 3 ml of MgCl2 (25 mM) and 12.3 ml of ddH₂O. The thermal cycling conditions were as follows: an initial period of 5 min at 95 ºC, followed by 35 cycles of 60 s at 95 °C, 1.2 min at 55 °C, 60 s at 72 °C, and as a final extension for 7 min at 72 °C. PCR products were sequenced at Washington University using an ABI 3730xl sequencer (Applied BiosystemsTM). All nucleotide sequences obtained were compared, edited manually with SequencherTM 4.7, and aligned with MAFFT (Katoh & Standley, 2013).

To describe the neutral variation of T. compacta, we estimated the total number of haplotypes, mutations, segregating sites (S), nucleotide diversity π, haplotype diversity (h) and the theta index of genetic diversity ϴ using the Nei’s (1987) equations implemented in DNAsp 5.1 (Rozas et al., 2003).

In order to compare the levels of genetic diversity among populations of T. compacta, we estimated the fixation index (F_ST) between populations using Arlequin v. 3.11 (Excoffier et al., 2005). To assess potential genetic clustering due to geographic distribution, we analyzed population structure using 2 methods. First, we used a Bayesian clustering analysis in BAPS for linked loci (Corander & Tang, 2007; Corander et al., 2008); we determined the number of genetic groups with the maximum likelihood value. We performed a mixture analysis with K values from 2 to 12, with 3 iterations each. Then, we used the output file to perform the admixture analysis. The minimum size of populations to be taken into account was set to 1, while 100 iterations were applied to estimate the admixture coefficients of individuals, 10 reference individuals from each population were used, and finally, 100 iterations were performed to estimate the admixture coefficients of the reference individuals. Second, we used a SAMOVA approach (spatial analysis of molecular variance; Dupanloup et al., 2002), which defines populations that are geographically homogeneous and maximally differentiated from each other.  We repeated the analyses with 2 (the minimum for SAMOVA) to 20 numbers of groups (K) until the F_CT value (the proportion of genetic variation among groups) reached a plateau. Each run consisted of 100 replications.

Table 1

Populations sampled of Trichobaris compacta and genetic diversity values estimated from COI gene. S segregating sites, h haplotype diversity, π nucleotide diversity and genetic diversity ϴ.

Number	State, Country	Locality code, host-plant	Coordinates	#  insects	# haplotypes	# mutations	S	# Singletons	h	π	ϴ
1	Arizona, USA	0Az, D. wrightii	32°35’32.79” N, 110°50’56.54” W	11	4	5	5	2	0.600	0.002	0.002
2	Arizona, USA,	1Az, D. wrightii	32°36’50.10” N, 110°49’57.91” W	12	7	6	6	5	0.833	0.001	0.003
3	Arizona, USA	2Az, D. wrightii	32°58’42.19” N, 110°46’8.08” W	8	6	5	5	4	0.893	0.002	0.002
4	Arizona, USA	3Az, D. wrightii	33°9’21.73” N, 111°46’36.77” W	10	9	14	13	11	0.945	0.004	0.007
5	Arizona, USA	4Az, D. wrightii	32°3’48.57” N, 110°17’3.42” W	15	8	8	8	7	0.848	0.002	0.003
6	Arizona, USA	6Az, D. wrightii	33°21’50.08” N, 112°37’32.06” W	10	5	7	7	5	0.822	0.002	0.003
7	Arizona, USA	7Az, D. wrightii	33°5’25.83” N, 112°2’1.26” W	2	1	0	0	0	0.000	0.000	0.000
8	California, USA	2SD, D. wrightii	33°34’26.50” N, 117°10’52.59” W	10	4	3	3	1	0.644	0.001	0.001
9	California, USA	3SD, D. wrightii	33°45’41.29” N, 117°11’27.19” W	8	1	0	0	0	0.000	0.000	0.000
10	California, USA	5SD, D. wrightii	33°46’4.14” N, 116°19’28.23” W	6	3	3	3	3	0.600	0.001	0.001
11	California, USA	6SD, D. wrightii	33°46’19.52” N, 116°19’53.98” W	1	1	0	0	0	0.000	0.000	0.000
12	California, USA	7SD, D. wrightii	33°35’42.08” N, 116°5’52.62” W	1	1	0	0	0	0.000	0.000	0.000
13	California, USA	8SD, D. wrightii	_____	3	3	5	5	5	1.000	0.005	0.005
14	California, USA	10SD, D. wrightii	34°6’52.93” N, 116°27’56.07” W	7	1	0	0	0	0.000	0.000	0.000
15	California, USA	11SD, D. wrightii	34°8’24.06” N, 116°24’48.14” W	6	1	0	0	0	0.000	0.000	0.000
16	California, USA	12SD, D. wrightii	33°5’38.23” N, 116°57’47.19” W	4	3	2	2	1	0.833	0.001	0.001
17	California, USA	13SD, D. wrightii	33°29’28.28” N, 117°3’28.97” W	4	3	3	3	3	0.833	0.002	0.002
18	California, USA	14SD, D. wrightii	33°29’1.49” N, 116°54’45.23” W	6	3	6	6	6	0.600	0.003	0.003
19	California, USA	15SD, D. wrightii	34°10’35.93” N, 116°25’36.47” W	12	4	6	6	4	0.636	0.002	0.003
20	California, USA	19SD, D. wrightii	34°15’18.02” N, 116°26’19.72” W	4	2	1	1	1	0.500	0.001	0.001
21	California, USA	20SD, D. wrightii	33°59’46.45” N, 116°34’43.69” W	5	2	1	1	1	0.400	0.001	0.001
Table 1. Continued
Number	State, Country	Locality code, host-plant	Coordinates	#  insects	# haplotypes	# mutations	S	# Singletons	h	π	ϴ
22	California, USA	21SD, D. wrightii	33°57’29.11” N, 116°35’30.66” W	2	2	2	2	2	1.000	0.003	0.003
23	Oaxaca, Mexico	314, D. discolor	16°47’11.61” N, 96 12’42.34” W	13	2	4	4	4	0.154	0.001	0.001
24	Oaxaca, Mexico	415, D. pruinosa	16°40’2.60” N, 96 22’48.98” W	18	2	1	1	0	0.366	0.001	0.000
25	Oaxaca, Mexico	516, D. inoxia	16°28’46.10” N, 96 13’3.51” W	19	2	1	1	0	0.281	0.001	0.001
26	Sonora, Mexico	828, D. discolor	32°11’28.14” N, 114 55’19.63” W	9	1	0	0	0	0.000	0.000	0.000
27	B.California, Mexico	129, D. discolor	26°0’21.46” N, 111 20’35.34” W	14	7	17	17	14	0.758	0.004	0.008
28	Oaxaca, Mexico	Oax, D. discolor	16°55’11.92” N, 96 23’6.10” W	3	1	0	0	0	0.000	0.000	0.000
29	Sinaloa, Mexico	OG, D. reburra	25°26’25.92” N, 108 3’59.49” W	9	5	7	7	5	0.833	0.003	0.003
			Total	232	49	57	56	33	0.704	0.002	0.014

The method is based on a simulated annealing procedure that aims to maximize the proportion of total genetic variance due to differences among groups of populations (F_CT). The most significant statistical output indicates the number of groups. Simulations have shown that the SAMOVA algorithm does indeed find maximally differentiated groups, especially when data are derived from a single locus.

To visualize the frequency and distribution of haplotypes, we constructed an un-rooted haplotype network using the Median-joining algorithm. This analysis was performed in Network v. 4.6.1.1. (Bandelt et al., 1999). A haplotype phylogeny was estimated with a Bayesian inference analysis in BEAST v.1.4.7 (Drummond & Rambaut, 2007). The parameters of MCMC runs were 30 million generations, sampling every 1,000 generations and discarding the first 10,000 trees as burn-in. We used a GTR+I model of nucleotide substitution and a fixed substitution rate of 2% per million years for COI, as previously reported for coleopterans (Nakamine & Takeda, 2008). To identify ancestral and derived haplotypes in the phylogeny, the trees were rooted using sequences of Trichobaris soror. We analyzed the sets of trees using DensiTree, showing only consensus trees (BEAST v.1.4.7 package software; Drummond & Rambaut, 2007).

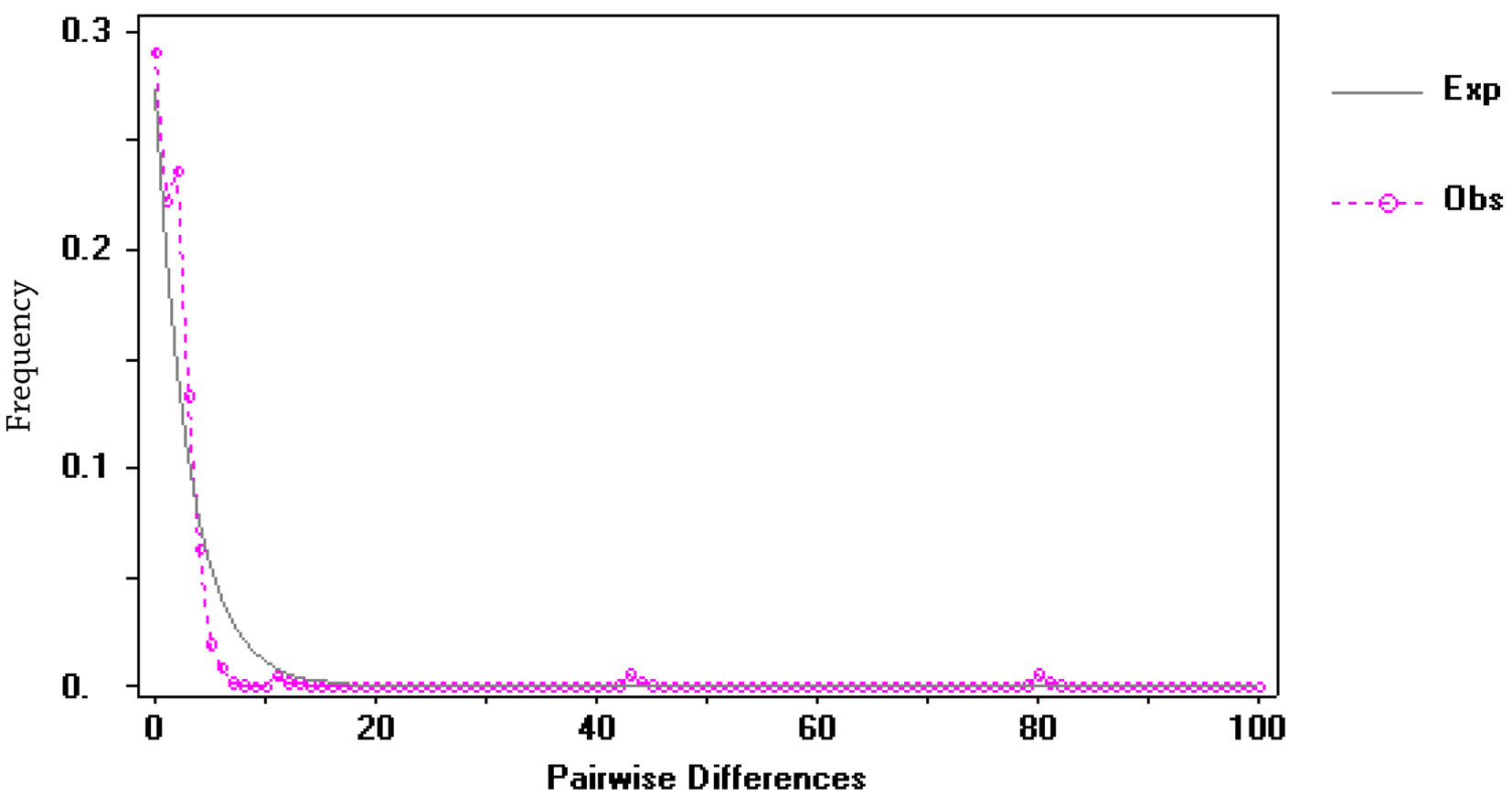
To determine whether demographic events have shaped the genetic variation of T. compacta, we estimated Fu and Li’s F (1993) and Tajima’s D statistics (Tajima, 1989). These estimators assume neutrality to infer population historical demography. The Tajima’s D statistic is expected to be negative when the genetic structure has been influenced by a rapid range expansion, positive when the population has passed through a bottleneck, and zero when there is an equilibrium between mutation and drift (Tajima, 1989). To compare the observed frequencies of pairwise differences with those expected under a model of demographic expansion, mismatch distributions were generated using DNAsp v.4.10 (Rozas et al., 2003). A multimodal distribution is expected when there are no changes affecting population size, but unimodal distributions are expected when sudden demographic expansions have occurred (Rogers & Harpending, 1992).

Table 2

Genbank accession numbers of haplotypes of Trichobaris compacta.

Genbank accession number	Haplotype number in this study
KX359683	Co33
KX359684	Co1
KX359685	Co37
KX359686	Co26
KX359687	Co6
KX359688	Co27
KX359689	Co35
KX359690	Co36
KX359691	Co8
KX359692	Co39
KX359693	Co23
KX359694	Co7
KX359695	Co22
KX359696	Co19
KX359697	Co5
KX359698	Co20
KX359699	Co48
KX359700	Co28
KX359701	Co32
KX359702	Co47
KX359703	Co49
KX359704	Co24
KX359705	Co38
KX359706	Co25
KX359707	Co2
KX359708	Co10
KX359709	Co14
KX359710	Co18
KX359711	Co15
KX359712	Co17
KX359713	Co16
KX359714	Co29
KX359715	Co9
KX359716	Co40
KX359717	Co30
KX359718	Co13
KX359719	Co31
KX359720	Co11
KX359721	Co41
KX359722	Co12
KX359723	Co34

Results

The southwest Mexico has not previously been reported as a distribution area of T. compacta (Barber, 1935), and most sampling was performed in the northern part of its distribution on D. wrightii and D. discolor (Table 1, from localities 1-22). However, in this study, we report new data for T. compacta distribution and host plant species: D. pruinosa, D. reburra and D. inoxia (Table 1, from localities 23-29). These populations were sampled in southwest Mexico (Fig. 1).

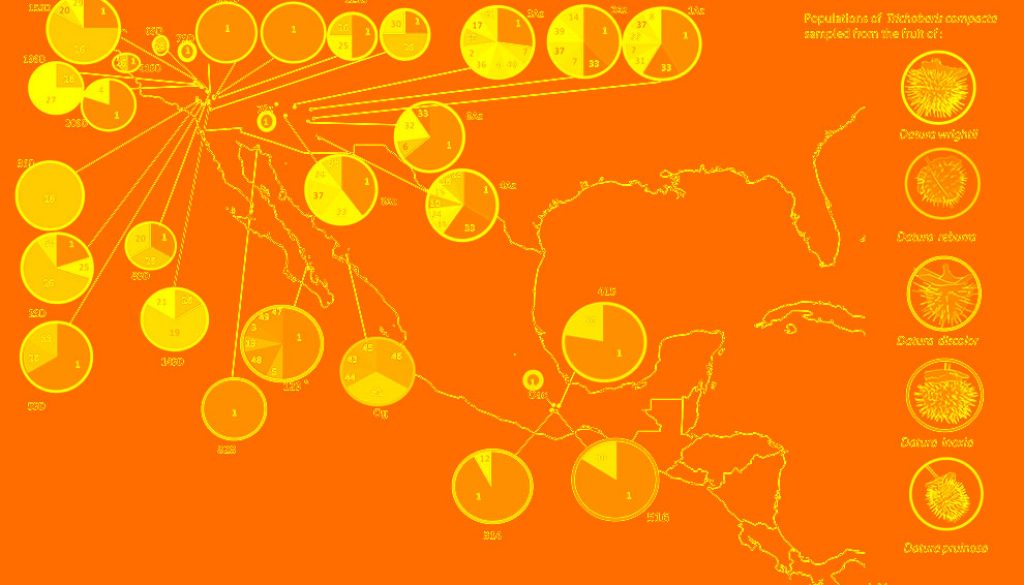
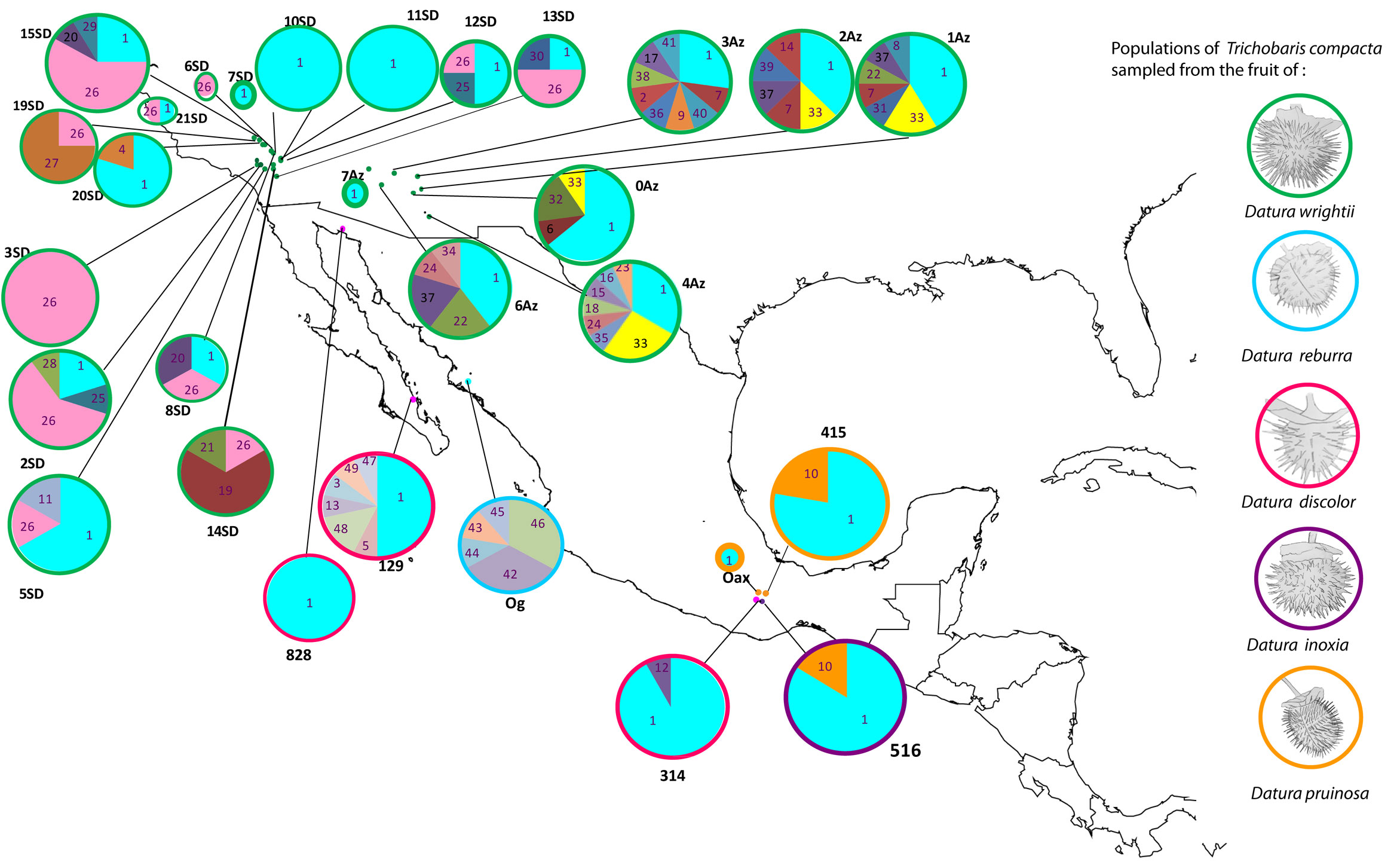
We found 49 haplotypes, 33 segregation sites (S), and 56 singletons (Table 1). Sequences without missing bases were submitted to GenBank (KX359683 to KX359723; Table 2). Trichobaris compacta possess high genetic diversity (h = 0.704, π = 0.002, ϴ = 0.014) (Table 1). The most common haplotype, Co1, is present in the entire distribution range of this weevil (Fig. 1).

A significant genetic differentiation among populations was detected. F_ST values range from 0.076 to 1.0 among populations. The most differentiated populations were 14SD, 19SD and 3SD (Table 3, Fig. 1), indicating that the haplotypes of this region are more exclusive along the distribution of T. compacta. The Bayesian clustering analysis performed with BAPS showed that the maximum likelihood value is reached at K = 3 (Fig. 2): cluster 1 in green, cluster 2 in yellow and cluster 3 in blue. Much of the genetic variation is specific to each group 1 (97%), group 2 (100%), and group 3 (87%) with very little gene flow between groups (for example, between group 3 and group 1 is only 1.1%). With SAMOVA, the highest value of F_CT was found at K = 3, p-value = 0.05083 ± 0.00800, the criterion for choosing this number of groups was the peak of F_CT before the plateau phase (after K = 9 and up to K = 20 values F_CT for which the analysis was run) (Table 4).

The most frequent and shared haplotypes among populations were Co1 (52% of total sampling), Co26 (13%), Co33 (3%), and Co10 (3%) (Figs. 1, 3). From these, Co1 and Co10 were sampled in more than 1 host-plant species (D. wrightii, D. discolor, D. inoxia and D. pruinosa), while 7 haplotypes were found exclusively in D. discolor, 5 in D. reburra and 35 in D. wrightii.

Phylogenetic analysis of COI haplotypes did not support the formation of main clades into T. compacta (Fig. 4). Posterior probability values lower than 0.50 are not show in the phylogeny, only 3 clades with 2 or 3 haplotypes have support higher to 0.90.

The haplotype network showed a star-like pattern indicative of a recent population expansion and congruent with both the mismatch distribution that displayed a unimodal pattern (Fig. 5) and with the negative values of Tajima’s D = -2.69330 (p < 0.001) and Fu and Li’s F = -5.10607 (p < 0.02).

Table 3

Population differentiation values Fst among sampling sites (at least n = 3) of Trichobaris compacta estimated from COI gene. The statistically significant values are indicated in bold type.

Fst	0Az	10SD	11SD	12SD	13SD	14SD	15SD	19SD	1Az	20SD	2Az	2SD
0Az	0.000
10SD	-0.024	0.000
11SD	-0.043	0.000	0.000
12SD	-0.073	0.378	0.336	0.000
13SD	0.021	0.685	0.656	0.030	0.000
14SD	0.147	0.599	0.571	0.418	0.500	0.000
15SD	0.114	0.429	0.408	-0.018	-0.113	0.457	0.000
19SD	0.176	0.938	0.931	0.583	0.333	0.683	0.294	0.000
1Az	-0.056	-0.050	-0.675	-0.100	-0.026	0.073	0.076	0.089	0.000
20SD	-0.061	0.073	0.040	0.206	0.542	0.490	0.371	0.850	-0.087	0.000
2Az	-0.013	0.028	0.004	0.120	0.418	0.453	0.361	0.682	-0.041	-0.006	0.000
2SD	0.135	0.635	0.616	0.100	-0.120	0.588	-0.053	0.380	0.085	0.560	0.485	0.000
314	0.035	-0.055	-0.072	0.231	0.577	0.578	0.436	0.808	0.005	-0.026	0.058	0.581
3Az	0.020	0.011	-0.001	0.046	0.276	0.350	0.299	0.506	-0.008	-0.021	-0.065	0.370
3SD	0.221	1.000	1.000	0.681	0.186	0.765	0.127	0.781	0.142	0.933	0.740	0.116
415	0.076	0.077	0.060	0.372	0.661	0.666	0.512	0.869	0.037	0.101	0.144	0.655
4Az	0.027	0.038	0.020	0.148	0.436	0.483	0.385	0.667	0.012	0.020	0.033	0.483
516	0.078	0.020	0.004	0.404	0.701	0.689	0.528	0.891	0.038	0.081	0.138	0.681
5SD	-0.047	0.028	0.000	-0.077	0.306	0.449	0.207	0.690	-0.066	-0.015	0.020	0.367
6Az	0.009	0.005	-0.015	0.096	0.383	0.433	0.349	0.635	-0.021	-0.020	-0.032	0.453
8SD	-0.108	0.300	0.250	-0.124	0.039	0.051	0.011	0.445	-0.140	0.142	0.122	0.210
854	0.003	0.000	0.000	0.445	0.731	0.644	0.465	0.949	-0.026	0.126	0.065	0.667
OG	0.464	0.811	0.799	0.740	0.756	0.760	0.765	0.814	0.358	0.770	0.742	0.801
129	0.034	-0.003	-0.020	0.034	0.257	0.330	0.283	0.478	0.010	-0.043	0.038	0.335
Fst	314	3Az	3SD	415	4Az	516	5SD	6Az	8SD	854	OG	129
314	0.000
3Az	0.066	0.000
3SD	0.836	0.546	0.000
415	0.082	0.125	0.887	0.000
4Az	0.080	0.065	0.686	0.144	0.000
516	0.050	0.122	0.909	-0.043	0.135	0.000
5SD	0.024	0.010	0.765	0.130	0.054	0.121	0.000
6Az	0.050	-0.003	0.677	0.121	0.024	0.114	0.013	0.000
8SD	0.271	0.051	0.587	0.411	0.182	0.444	0.000	0.111	0.000
854	-0.031	0.041	1.000	0.103	0.065	0.044	0.072	0.037	0.379	0.000
OG	0.813	0.667	0.860	0.853	0.751	0.863	0.755	0.733	0.693	0.832	0.000
129	0.052	0.061	0.504	0.100	0.087	0.096	0.002	0.051	0.045	0.024	0.666	0.000

Table 4

Results from SAMOVA analysis of Trichobaris compacta populations, using COI gene (663bp). K = arbitrary partition of the n populations into K groups, F_CT = index of genetic variance due to differences among populations, p-value = probability values to accept the new structure.

K	1	2	3	4	5
FCT	.	0.21845	0.29099	0.25082	0.24094
p-value	.	0.02639+-0.00439	0.05083+-0.00800	0.01466+-0.00394	0.02151+-0.00491
K	6	7	8	9	10
FCT	0.22482	0.23485	0.21917	0.38133	0.37744
p-value	0.03128+-0.00620	0.04594+-0.00610	0.07820+-0.00897	0.00098+-0.00098	0.00000+-0.00000
K	11	12	13	14	15
FCT	0.3733	0.38933	0.34445	0.34587	0.36122
p-value	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000
K	16	17	18	19	20
FCT	0.35109	0.35171	0.36861	0.38472	0.36474
p-value	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000	0.00000+-0.00000

Discussion

In general, the COI sequence of weevils shows high levels of genetic variation (from 0.973 to 0.75) allowing to discern different evolutionary lineages and population structure of this species (Anducho-Reyes et al., 2008; Aoki et al., 2008, 2009; Kuester et al., 2012; Ruiz et al., 2010). Here, we show that T. compacta have also higher level of genetic variation (h = 0.704) distributed mainly in the northern part of its distribution, USA, than in the south (Table 1; Fig. 1). Trichobaris soror, a weevil of the same genus but species-specific to a host plant and distributed on the highlands of Mexico, showed a similar level of genetic variation, h = 0.731 (De la Mora et al., 2015). Trichobaris compacta diverged from T. soror ca. 1.75 (± 1) million years ago, with a recent diversification ca. 0.5 (± 0.25) million years ago (De la Mora et al., 2018).

Neutral theory postulates that genetic diversity will increase with larger effective population sizes due to a decreasing effect of genetic drift (Kimura, 1983). According to the specialist-generalist variation hypothesis (SGVH), specialists are expected to have lower effective population sizes than generalists and consequently lower levels of genetic diversity due to the effect of drift (Li et al., 2014). This pattern may result from their specialization in resource use; for instance, the habitat of specialist species may be more heterogeneous and patchier than that of generalists and, as a consequence, populations of specialist species may be less connected and more subdivided into smaller populations than those of generalist species. Therefore, we expected that the generalist T. compacta, which uses several host-plant species to feed and reproduce, would have higher levels of genetic variation than a specialist weevil. However, although Trichobaris soror feeds only on D. stramonium, our estimate of genetic diversity does not differ between species of Trichobaris. Therefore, no support for this hypothesis was found. It is likely that since the host plant of T. soror (D. stramonium) is highly abundant but with a patchy distribution along the Trans-Mexican Volcanic Belt, this has promoted high genetic variation of similar magnitude to that of T. compacta. However, the role of trophic host specialization and the distribution pattern of both species of Trichobaris on their genetic variation remains to be tested.

Phylogenetic structure. The population genetic structure of T. compacta investigated with COI does not reflect a significant genetic clustering, since the same haplotype can be found from Arizona in the USA, to Oaxaca in central Mexico. As mentioned below, a slight influence of the Colorado River basin may be disrupting the genetic flow in T. compacta. It is a bit difficult to compare the compact phylogeographic pattern of T. compacta with other insects since phylogeographic studies are scarce, in spite that other insect species distribute in the same geographical range (Anderson & O’Brien, 1996). Unlike T. compacta, T. soror is distributed only along the Trans-Mexican Volcanic Belt and in the Sierra Madre del Sur (Barber, 1935). The phylogeographical pattern of T. soror follows a partition due to the mountain systems, similar to other beetles distributed on the same region (i.e., Dendroctonus mexicanus; Anducho-Reyes et al., 2008).

Other taxa distributed in North American warm deserts have revealed vicariant events among their populations distributed in this area (Bryson et al., 2012; Leache & Mulcahy, 2007; Mantooth et al., 2013), and the barriers to gene flow for this biota have been identified as the Central Valley, the Colorado River and floristic provinces. At the equatorial climate, along the western coast of Mexico, Neotropical biota have been greatly influenced by past events that have produced strong genetic differentiation within species (García-Trejo et al., 2004; Zarza et al., 2008). We expected that at least the genetic variation of T. compacta would reflect these discontinuities. However, the genetic groups do not correspond to either the desert typical barriers or to a disjunction between the desert and equatorial climates. The Colorado River system seems to have slightly influenced the population structure of T. compacta because of the different haplotypic compositions found at each side (Fig. 2). However, the results of BAPS and SAMOVA do not support this barrier and estimations of gene flow are needed to corroborate this. Both analyzes suggest the formation of 3 groups but these groups are not equivalent. In BAPS there is a widely distributed group (cluster2-yellow) that includes several populations from the north and mainly from the south of the distribution (Fig. 2). While the other 2 form some geographical structure to the north of the T. compact distribution, SD populations in San Diego (cluster 1-green) and AZ populations in Arizona (cluster 3-blue). In SAMOVA, the K = 3 populations were grouped as: group 1 (0Az, 10SD, 11SD, 12SD, 13SD, 15SD, 1Az, 20SD, 2Az, 2SD, 314, 3Az, 405, 4Az, 516, 5SD, 6Az, 8SD, AP, OG, 129) group 2 (19SD, 3SD) and group 3 (14SD). Although the SAMOVA results, in general, were not statistically significant (Table 4), K = 3 was the peak of F_CT and was marginally significant. It is likely that T. compacta is broadly distributed over the Datura species that we report in Mexico and gene flow is maintained along their distribution; yet extensive sampling to delimit the distribution of T. compacta in all 5 Datura species is badly needed.

The distribution of haplotypes is not uniform in all Datura species (Fig. 1). The most frequent haplotype of T. compacta (Co1) was found on 4 species of Datura distributed in USA and Mexico. All other haplotypes were found in D. wrightii and D. discolor, but some low-frequency haplotypes were restricted to D. reburra, D. pruinosa and D. inoxia. The haplotype network shows few mutational steps among haplotypes, which suggests a recent divergence of the haplotypes, but none of these as previously reported is associated to particular Datura species (De la Mora et al., 2018; Fig. 3).

Because plant-herbivore interactions have largely been maintained since the last glacial period, variation in mtDNA results useful to infer clades association to particular host plants (Aoki et al., 2011). Like results reported in other weevil species with larval development inside the host plant tissues (Aoki et al., 2009; Barr et al., 2013), we expected to find the COI gene haplotypes of T. compacta linked to different Datura species and clustered together with high support by a phylogeny, but we did not find such a pattern (Figs. 4, 5). The neutral nature of COI variation, in relation to host plant use made by weevils, does not mean that T. compacta is not adapted to Datura species. We are unable to assess adaptation to the host plant directly (Barr et al., 2013; Morse & Farrell, 2005). If weevils were adapted to host plants, analysis of other loci that code for adaptive traits to host plants and behavioral experiments of oviposition would be necessary. Rather, we determined that the relationship between T. compacta and Datura species is not reflected by clustering of mtDNA lineages linked to particular host plant species. It is possible that T. compacta had recently dispersed to Datura host species until attaining its current distribution range, as suggested by both the star-like pattern of the haplotype network and the historical-demographic analysis.

In the insect-plant interaction study, the phylogenetic study of variation in the COI gene revealed that interacting species share patterns of neutral genetic variation because they have been exposed to the same environmental and geological conditions (Aoki et al., 2009, 2011). In this sense, this study constitutes one of the first steps to understand the coevolution of Trichobaris with
Datura species.

Phylogeographic and phylogenetic analyses showed that T. compacta populations are slightly structured over a wide geographic distribution range. This genetic population structure is the result of the admixture of tree genetic groups, forming a single one genealogical lineage.

Acknowledgments

To R. Tapia-López for her technical support and A. Miranda-Pérez for their assistance during field collection. We thank the reviewers for their helpful comments on the manuscript. Funding was provided by PAPIIT-UNAM (AG-200717) and Conacyt grant Fronteras 1527. M. De la Mora acknowledges the scholarship from Conacyt for graduate studies. This contribution is part of the Ph. D. thesis of De la Mora in the Posgrado en Ciencias Biológicas, UNAM.

References

Anderson, R. S., & O’Brien, C. W. (1996). Curculionidae (Coleoptera). Biodiversidad, taxonomía y biogeografía de artrópodos de México: hacia una síntesis de su conocimiento. México D.F.: Instituto de Biología, Universidad Nacional Autónoma de México.

Anducho-Reyes, M. A., Cognato, A. I., Hayes, J. L., & Zúñiga, G. (2008). Phylogeography of the bark beetle Dendroctonus mexicanus Hopkins (Coleoptera: Curculionidae: Scolytinae). Molecular Phylogenetics and Evolution, 49, 930–940. https://doi.org/10.1016/j.ympev.2008.09.005

Aoki, K., Kato, M., & Murakami, N. (2008). Glacial bottleneck and postglacial recolonization of a seed parasitic weevil, Curculio hilgendorfi, inferred from mitochondrial DNA variation. Molecular Ecology, 17, 3276–3289. https://doi.org/10.1111/j.1365-294X.2008.03830.x

Aoki, K., Kato, M., & Murakami, N. (2009). Phylogeographical patterns of a generalist acorn weevil: insight into the biogeographical history of broadleaved deciduous and evergreen forests. BMC Evolutionary Biology, 9, 103. https://doi.org/10.1186/1471-2148-9-103

Aoki, K., Kato, M., & Murakami, N. (2011). Phylogeography of phytophagous weevils and plant species in broadleaved evergreen forests: a congruent genetic gap between western and eastern parts of Japan. Insects, 2, 128–150. https://doi.org/10.3390/insects2020128

Avise, J. C. (2004).  Molecular markers, natural history, and evolution, Second Edition. Sunderland, MA.: Sinauer.

Bandelt, H. J., Forster, P., & Röhl, A. (1999). Median-joining networks for inferring intraspecific phylogenies. Molecular Biology and Evolution, 16, 37–48. https://doi.org/10.1093/oxfordjournals.molbev.a026036

Barber, H. S. (1935). The tobacco and solanum weevils of the genus Trichobaris. Miscellaneous Publication No. 226. Washington D.C.: United States Department of Agriculture.

Barr, N., Ruiz-Arce, R., Obregón, O., De León, R., Foster, N., Reuter, C. et al. (2013). Molecular diagnosis of populational variants of Anthonomus grandis (Coleoptera: Curculionidae) in North America. Journal of Economic Entomology, 106, 437–449. https://doi.org/10.1603/EC12340

Bryson, R. W., Jaeger, J. R., Lemos-Espinal, J. A., & Lazcano, D. (2012). A multilocus perspective on the speciation history of a North American aridland toad (Anaxyrus punctatus). Molecular Phylogenetics and Evolution, 64, 393–400. https://doi.org/10.1016/j.ympev.2012.04.014

Corander, J., & Tang, J. (2007). Bayesian analysis of population structure based on linked molecular information. Mathematical Biosciences, 205, 19–31. https://doi.org/10.1016/j.mbs.2006.09.015

Corander, J., Marttinen, P., Sirén, J., & Tang, J. (2008). Enhanced Bayesian modelling in BAPS software for learning genetic structures of populations. BMC Bioinformatics, 9, 539. https://doi.org/10.1186/1471-2105-9-539

De la Mora, M., Piñero, D., & Núñez-Farfán, J. (2015). Phylogeography of specialist weevil Trichobaris soror: a seed predator of Datura stramonium. Genetica, 143, 681–691. https://doi.org/10.1007/s10709-015-9866-x

De la Mora, M., Piñero, D., Oyama, K., Farrell, B., Magallón, S., & Núñez-Farfán, J. (2018). Evolution of Trichobaris (Curculionidae) in relation to host plants: Geometric morphometrics, phylogeny and phylogeography. Molecular Phylogenetics and Evolution, 124, 37–49. https://doi.org/10.1016/j.ympev.2018.02.018

Diezel, C., Allmann, S., & Baldwin, I. T. (2011). Mechanisms of optimal defense patterns in Nicotiana attenuata: flowering attenuates herbivory‐elicited Ethylene and Jasmonate Signaling F. Journal of Integrative Plant Biology, 53, 971–983. https://doi.org/10.1111/j.1744-7909.2011.01086.x

Drummond, A. J., & Rambaut, A. (2007). BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evolutionary Biology, 7, 214. https://doi.org/10.1186/1471-2148-7-214

Dupanloup, I., Schneider, S., & Excoffier, L. (2002). A simulated annealing approach to define the genetic structure of populations. Molecular Ecology, 11, 2571–2581. http://doi.org/10.1046/j.1365-294X.2002.01650.x

Dupin, J., Matzke, N. J., Särkinen, T., Knapp, S., Olmstead, R. G., Bohs, L. et al. (2016). Bayesian estimation of the global biogeographical history of the Solanaceae. Journal of Biogeography, 44, 887–899. http://doi.org/10.1111/jbi.12898

Excoffier, L., Laval, G., & Schneider, S. (2005) Arlequin (version 3.0): An integrated software package for population genetics data analysis. Evolutionary Bioinformatics Online, 1, 47–50. http://doi.org/10.1177/117693430500100003

Fu, Y. X., & Li W-H. (1993) Statistical test of neutrality mutations. Genetics, 147, 915–923. https://doi.org/10.1093/genetics/133.3.693

García-Trejo, E. A., Navarro, S., & Adolfo, G. (2004). Patrones biogeográficos de la riqueza de especies y el endemismo de la avifauna en el oeste de México. Acta Zoológica Mexicana, 20, 167–185. https://doi.org/10.21829/azm.2004.2022336

Halffter, G. (1976). Distribución de los insectos en la Zona de Transición Mexicana. Relaciones con la entomofauna de Norteamérica. Folia Entomológica Mexicana, 35, 1–64.

Katoh, K., & Standley, D. M. (2013). MAFFT multiple sequence alignment software version 7: improvements in performance and usability. Molecular Biology and Evolution, 30, 772–780. https://doi.org/10.1093/molbev/mst010

Kimura, M. (1983). The neutral theory of molecular evolution. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511623486

Kuester, A. P., Jones, R. W., Sappington, T. W., Kim, K. S., Barr, N. B., Roehrdanz, R. L. et al. (2012). Population structure and genetic diversity of the boll weevil (Coleoptera: Curculionidae) on Gossypium in North America. Annals of the Entomological Society of America, 105, 902–916. https://doi.org/10.1603/AN12072

Leache, A. D., & Mulcahy, D. G. (2007). Phylogeny, divergence times and species limits of spiny lizards (Sceloporus magister species group) in western North American deserts and Baja California. Molecular Ecology, 16, 5216–5233. https://doi.org/10.1111/j.1365-294X.2007.03556.x

Li, S., Jovelin, R., Yoshiga, T., Tanaka, R., & Cutter, A. D. (2014). Specialist versus generalist life histories and nucleotide diversity in Caenorhabditis nematodes. Proceedings of the Royal Society of London B: Biological Sciences, 281, 20132858. https://doi.org/10.1098/rspb.2013.2858

Luna-Cavazos, M., & Bye, R. (2011). Phytogeographic analysis of the genus Datura (Solanaceae) in continental Mexico. Revista Mexicana de Biodiversidad, 82, 977–988. http://dx.doi.org/10.22201/ib.20078706e.2011.3.720

Mantooth, S. J., Hafner, D. J., Bryson, R. W., & Riddle, B. R. (2013). Phylogeographic diversification of antelope squirrels (Ammospermophilus) across North American deserts. Biological Journal of the Linnean Society, 109, 949–967. https://doi.org/10.1111/bij.12084

Morrone, J. J. (2015). Halffter’s Mexican transition zone (1962–2014), cenocrons and evolutionary biogeography. Journal of Zoological Systematics and Evolutionary Research, 53, 249–257. https://doi.org/10.1111/jzs.12098

Morse, G. E., & Farrell, B. D. (2005). Ecological and evolutionary diversification of the seed beetle genus Stator (Coleoptera: Chrysomelidae: Bruchinae). Evolution, 59, 1315–1333. https://doi.org/10.1111/j.0014-3820.2005.tb01782.x

Nakamine, H., & Takeda, M. (2008) Molecular phylogenetic relationships of flightless beetles belonging to the genus Mesechthistatus Breuning, (Coleoptera: Cerambycidae) inferred from mitochondrial COI sequences. Journal of Insect Science, 8, 1–11. https://doi.org/10.1673/031.008.7001

Nei, M. (1987). Molecular evolutionary genetics. New York: Columbia University Press. https://doi.org/10.7312/nei-920
38-005

Rogers, A. R., & Harpending, H. (1992). Population growth makes waves in the distribution of pairwise genetic differences. Molecular Biology and Evolution, 9, 552–569. https://doi.org/10.1093/oxfordjournals.molbev.a040727

Rozas, J., Sánchez-DelBarrio, J. C., Messeguer, X., & Rozas, R. (2003). DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics, 19, 2496–2497. https://doi.org/10.1093/bioinformatics/btg359

Ruiz, E. A., Rinehart, J. E., Hayes, J. L., & Zúñiga, G. (2010). Historical demography and phylogeography of a specialist bark beetle, Dendroctonus pseudotsugae Hopkins (Curculionidae: Scolytinae). Environmental Entomology, 39, 1685–1697. https://doi.org/10.1603/EN09339

Sota, T., Hayashi, M., & Iwai, D. (2004). Phylogeography of the leaf beetle Chrysolina pectina in wetlands of Japan inferred from the distribution of mitochondrial haplotypes. Entomological Science, 7, 381–388. https://doi.org/10.1111/j.1479-8298.2004.00087.x

Tajima, F. (1989). Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics, 123, 585–595.

Zarza, E., Reynoso, V. H., & Emerson, B. C. (2008). Diversification in the northern neotropics: mitochondrial and nuclear DNA phylogeography of the iguana Ctenosaura pectinata and related species. Molecular Ecology, 17, 3259–3275. https://doi.org/10.1111/j.1365-294X.2008.03826.x