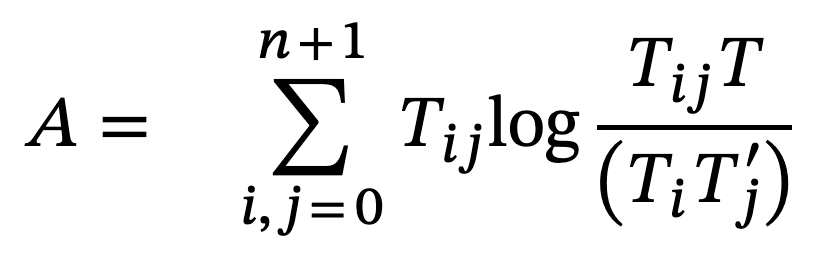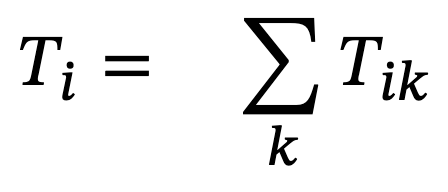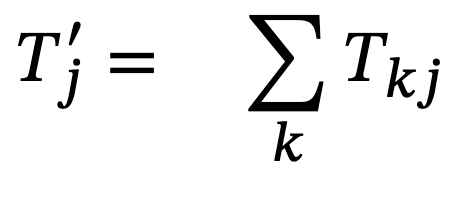Redes tróficas como herramienta para el estudio de la diversidad y complejidad de ecosistemas

Food webs as a tool for the study of diversity and complexity of ecosystems

Abstract

La Física y la Química están consideradas como “ciencias duras”, principalmente, porque utilizando el método científico son capaces de desarrollar leyes a partir de teorías con las que los fenómenos naturales pueden ser modelados y así predecir en tiempo y/o espacio particularidades de éstos. La ecología, por otro lado, ha recibido fuertes críticas por su falta de certeza en la predicción de eventos naturales, aunque en años recientes los enfoques de investigación están plagados de procesos de modelación matemática aplicada a la ecología (e.g., DeAngelis, 2018). Un ejemplo de ello es el desarrollo de predicciones con una menor incertidumbre en el área de la ecología de poblaciones utilizando modelos estocásticos (e.g., métodos de Monte Carlo) y otros modelos relacionados con la interacción depredador-presa (Sinclair et al., 1998). Sin embargo, al pasar a niveles de mayor complejidad, por ejemplo, en relaciones de más de 5 especies, comunidades y ecosistemas, la situación es distinta. El principal problema de que los modelos ecológicos no predigan de manera eficaz fenómenos naturales se debe a la complejidad intrínseca de los propios sistemas que se requiere estudiar. Ejemplo de ello es el comportamiento intricado en 2 dimensiones (espacio-tiempo) de las variables que origina una gran incertidumbre al tratar de modelar las variaciones asociadas. Esta incertidumbre es alta produciendo resultados difíciles de manejar en la mayoría de los casos aunados al efecto sinérgico y las propiedades emergentes de las interacciones entre los componentes bajo estudio. Ulanowicz (2009) escribe: “Los mecanismos están en el corazón de la modelación ecológica y la suposición tácita ha sido un creciente catálogo de varios mecanismos que eventualmente conducirán a los ecólogos a formular generalizaciones, parecidas a leyes del comportamiento del ecosistema” ¿Pero tales leyes existen en ecología? se pregunta Fox-Keller (2007). 

El presente escrito no pretende ser una compilación exhaustiva de la historia del análisis de redes tróficas, ni tampoco pretende hacer una lista de las distintas metodologías utilizadas en su análisis, su objetivo principal es que el lector conozca de manera general la respuesta de 4 sencillas preguntas: ¿qué es una red trófica? ¿cómo se construye? ¿qué problemas pueden resolver? y ¿cómo interpretar los resultados a través de una visión global del análisis de redes tróficas? La ecología como otras ciencias, pretende determinar patrones de comportamiento de los fenómenos naturales, tanto a nivel temporal como espacial. Analizando las variables que determinan estos patrones y sus tendencias, es posible medir su variación y así modelar el comportamiento a través del análisis de estocasticidad. Esto resulta medular para estudios a nivel de ecosistema, donde cada especie tiene un comportamiento particular y reacciona a las variables ambientales de manera distinta (e.g., otras especies, temperatura, salinidad). 

Uno de los enfoques que se está explorando para analizar a las comunidades y ecosistemas, son las redes tróficas (Trifonova et al., 2015). Estas representan las interacciones depredador-presa, es decir, quién se come a quién y se trata de incluir a todas las especies muestreadas (o al menos los grupos taxonómicos más importantes) en un determinado tiempo y espacio. Por lo mismo, el análisis de las redes tróficas provee un medio para analizar la relación entre estructura, dinámica y funcionamiento del ecosistema, así como la forma en que están influenciadas por los disturbios y cambios ambientales.

Las redes tróficas pueden ser construidas de 2 formas: no ponderadas y ponderadas. Las primeras consideran únicamente la relación depredador-presa, sin incluir la cantidad de materia que fluye entre las especies, dentro de esta categoría está también la red bipartita. El segundo tipo considera la cantidad de materia que fluye entre las especies debido a la depredación, exportación, importación y desechos. A continuación, haremos una descripción de cada tipo considerando los métodos de construcción, su análisis y las ventajas y desventajas de cada una.

Redes tróficas no ponderadas

La construcción de una red trófica no ponderada parte del conocimiento de la alimentación de un conjunto de especies (fig. 1). Este conocimiento, generalmente, se adquiere al realizar los análisis de contenidos estomacales de depredadores de una comunidad, observaciones en campo, examen de excretas, análisis de isótopos estables o análisis de ADN de las presas. Los tipos alimenticios se enlistan y se relacionan con su depredador en una tabla o matriz de interacción llamada “adyacente”. En esta matriz, las columnas representan a los depredadores y los renglones a sus presas. Por ejemplo, la figura 1 muestra una red trófica en la que el halcón se alimenta del gorrión, quien a su vez se alimenta de la araña y ésta del saltamontes. En el ejemplo, el halcón es el depredador mientras que el gorrión es la presa, que a su vez es el depredador de la araña. La tabla 1 muestra esta misma red trófica de forma matricial, en la que los renglones son las presas y las columnas los depredadores, nótese que el número de columnas y renglones es el mismo.

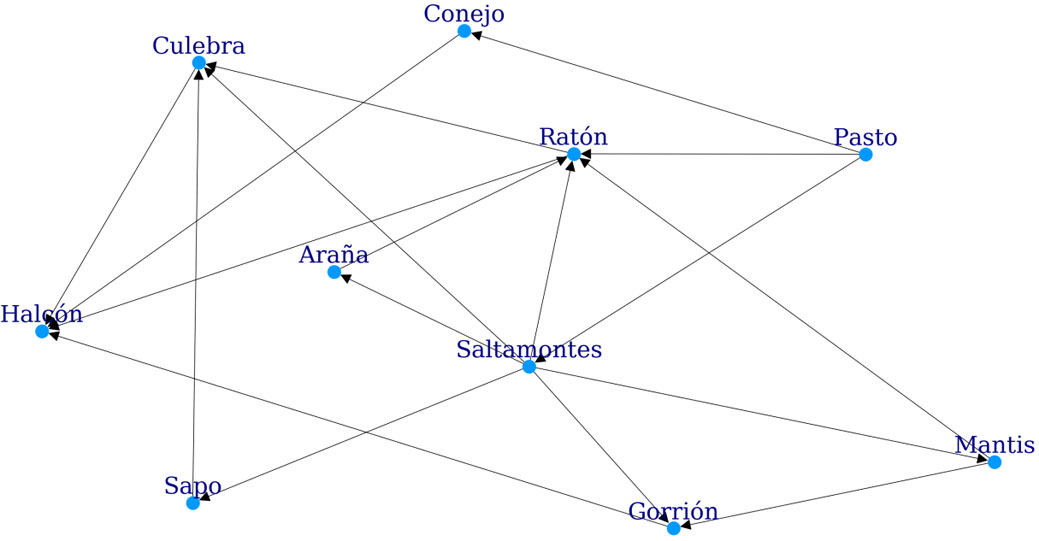
Para poder hacer un análisis completo es necesario que la matriz sea cuadrada, lo que implica que el conocimiento de los tipos alimenticios de las presas debe incorporarse a la matriz. Es decir, cuáles son las presas del alimento de la especie en cuestión a menos que se trate de una especie autótrofa. En este caso, lo que generalmente sucede es realizar una búsqueda bibliográfica de los hábitos alimenticios de la presa. Esta búsqueda se hace de manera tal, que si se conoce la especie, se busca su información, en caso de no encontrar datos, se amplía la búsqueda al género o familia. Es importante que se alcance la mejor resolución taxonómica posible y también es preferible que los resultados encontrados sean de la zona de interés. Existen muchos casos en los que no hay datos por lo que se hace una aproximación de alguna otra especie o género similar. 

Ya con la información completa, la matriz adyacente se llena con 0 en aquella celda en la que no existe depredación de la presa y con 1 en los casos en los que un depredador se alimenta de determinada presa, como se muestra en la tabla 1. Esta metodología es la más sencilla para organizar la red trófica y a partir de ésta se realizarán una serie de análisis estructurales y de funcionamiento que serán explicados brevemente más adelante.

Las redes tróficas no ponderadas han sido utilizadas desde hace ya algunas décadas como un modelo para el estudio de varios aspectos ecológicos de comunidades y ecosistemas. Una de las propuestas que mayor controversia ha generado, es la publicada por May en 1972 (véase también May, 1974), quien a partir de la generación al azar de interacciones entre especies y el nivel del efecto de éstas entre sí, hace un análisis de estabilidad del sistema. El resultado de las distintas simulaciones con varios escenarios respecto al número de especies y el grado de interacción entre las mismas, fue que mientras mayor es el número de especies en un ecosistema menor será la estabilidad de éste. Los resultados de May (1972, 1982) van en contra de lo observado en la naturaleza, donde cientos de especies se pueden encontrar conviviendo en una aparente estabilidad. Posteriormente y a la luz de los resultados contradictorios entre realidad y simulación, Pimm (1979, 1982), entre otros, llevó a cabo simulaciones de sistemas ecológicos con características más apegadas a los sistemas naturales. Los resultados de estos trabajos contradicen las conclusiones de May, generando, además, un auge en el estudio de la relación entre diversidad y estabilidad en ecosistemas.

Tabla 1

Representación de la red trófica de la figura 1 en la que los renglones representan las presas y las columnas los depredadores. Por ejemplo, el ratón, que es presa de la culebra y el halcón, en ese renglón tiene un número 1 en la columna de la culebra y el halcón. Esta matriz se conoce como matriz adyacente.

	Pasto	Saltamontes	Ratón	Conejo	Gorrión	Araña	Mantis	Sapo	Culebra	Halcón
Pasto	0	1	1	1	0	0	0	0	0	0
Saltamontes	0	0	1	0	1	1	1	1	1	0
Ratón	0	0	0	0	0	0	0	0	1	1
Conejo	0	0	0	0	0	0	0	0	0	1
Gorrión	0	0	0	0	0	0	0	0	0	1
Araña	0	0	1	0	0	0	0	0	0	0
Mantis	0	0	1	0	1	0	0	0	0	0
Sapo	0	0	0	0	0	0	0	0	1	0
Culebra	0	0	0	0	0	0	0	0	0	1
Halcón	0	0	0	0	0	0	0	0	0	0

Ya que la discusión sobre la relación diversidad–estabilidad comenzó, hubo un incremento de la compilación de datos sobre relaciones tróficas entre especies para comunidades y ecosistemas de distintas latitudes y tipos. A partir de estos trabajos, Cohen (1978) y Cohen et al. (1990), publicaron una compilación de más de 100 redes tróficas. Las redes tróficas comprenden varias décadas de estudios, algunas adaptaciones de trabajos de mediados de la década de 1920 y otras cercanas a la fecha de su publicación. A partir de la primera publicación de Cohen (1978), el crecimiento de artículos científicos relacionados con redes tróficas es casi exponencial (e.g., Ings et al., 2009). Una búsqueda en Google Scholar con las palabras “food web” en mayo del 2021 para el intervalo de años 2011 al 2020, resultó en 1,950,000 datos, lo que muestra el crecimiento en el estudio de esta línea de investigación muchas veces relacionada con otras líneas.

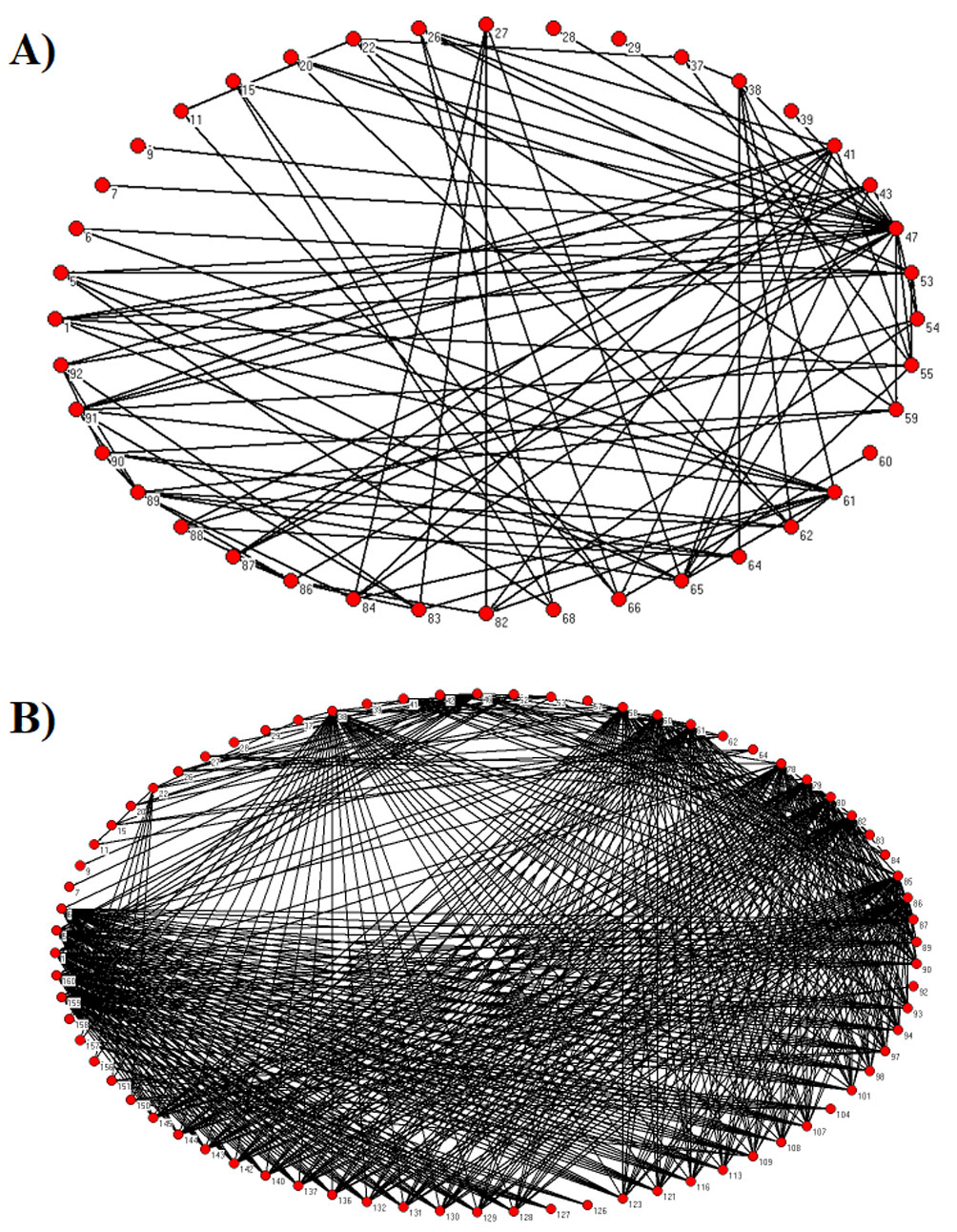
Una crítica a la base de datos de Cohen (1978) es el hecho de que el número de especies que conforman las redes tróficas no representa correctamente al ecosistema en cuestión, es decir, hay un problema de escala o resolución (Abarca-Arenas y Ulanowicz, 2002; Hall y Rafaelli, 1991; Martinez, 1991, 1993; Olivier y Palanque, 2017; Sugihara et al., 1989, 1997; Turney y Buddle, 2016; fig. 2). Esto implica que la interacción entre especies es incompleta y por lo mismo las aproximaciones realizadas por Cohen (1978) y Cohen et al. (1990) fueron sesgadas. Patonai y Jordán (2017) comparan distintos métodos de agregación en una red trófica y comparan los resultados de acuerdo con el número de especies. La sensibilidad de los resultados está relacionada con qué especies se agregan —similar a lo expuesto por Abarca-Arenas y Ulanowicz, 2002— lo que ayuda a entender qué especies o grupos necesitan mayor estudio de sus relaciones tróficas. Como ejemplo del efecto de disminuir la resolución de los nodos en una red se presenta la figura 2. La primera red (fig. 2A) es la representación de una red trófica en la que los nodos corresponden a especies agrupadas, por ejemplo: fitoplancton, zooplancton, bentos y peces. Por el contrario, en la figura 2B se representa la misma red trófica, pero cada nodo corresponde a una especie o al menos a varias especies de un mismo género. El número de especies y uniones son características importantes en la estructura de la red y por lo tanto las variaciones en su número tienen efectos en la interpretación de los resultados estructurales finales. En tabla 1 de material suplementario se presentan varios sitios repositorios de cientos de redes tróficas de distintos tipos y lugares del mundo que pueden ser consultadas y utilizadas libremente. Así mismo, se presenta una lista descriptiva de programas de cómputo que se utilizan para el análisis de redes tróficas. 

Una vez que los datos están listos para su análisis en forma de matriz, el siguiente paso es determinar la estructura de la red trófica. Este análisis mostrará, entre otras cosas, cuál o cuáles nodos son los que consumen presas en mayor o menor cantidad, cuál es el nivel trófico de cada especie o el nivel de omnivoría de cada especie y del sistema. A continuación, se describen brevemente algunos de los índices que se utilizan para el análisis estructural de redes tróficas.

Métodos de análisis

La estructura de una red, también conocida como la topología de la red, representa la forma en la que se arreglan los elementos de eésta, en nuestro caso las especies y su relación depredador-presa. Los aspectos que se han estudiado en cuanto a la estructura de redes tróficas provienen en su gran mayoría de los análisis realizados para redes sociales, que se tomaron de los análisis topológicos de redes estudiadas por los matemáticos (Barabási, 2002; Borgatti et al., 2009; Scott, 2000; Wasserman y Faust, 1994). 

Definiremos L como el número de uniones o relaciones que hay en toda la red, ésto es, la suma de “1” en la matriz adyacente y S como el número de especies o compartimentos de la red. La densidad de uniones es la proporción de uniones por especie y se calcula como L/S, es decir, en promedio cuántas uniones hay por especie en la red. Al comparar varias redes tróficas, la relación que existe entre la densidad de uniones con respecto a la riqueza de especies resulta en una de tipo log-log positiva con una alta correlación. No se observan valores extremos lo que significa que sin importar el tipo de ecosistema del que se trate, al incrementarse el número de especies hay un aumento considerable en el número de uniones promedio (Dunne, 2002; Martinez, 1992; Roopnarine et al., 2007). 

Otro parámetro común es la conectividad (C), que representa la proporción de uniones observadas entre las especies (L) y el máximo de uniones posibles de acuerdo con la riqueza de especies (S²), de tal forma que C = L/S². El parámetro de conectividad tomó importancia porque es uno de los que usó May (1972) para demostrar la inestabilidad de redes con un gran número de especies. Se ha demostrado que el comportamiento de C respecto al número de especies es de tipo log-log negativo y que, dependiendo de la resolución de las redes y en algunos casos, del tipo de sistemas que se trate, varía el valor negativo del exponente (Digel et al., 2014; Martinez, 1992; Riede et al., 2010; Vermaat et al., 2009; Yen et al., 2016). 

El nivel trófico de las especies que componen una red es importante para determinar, entre otras cosas, la eficiencia de la transferencia de materia entre las mismas (Cohen et al., 2003). El nivel trófico de una especie depende de la proporción de alimento que ingiere por cada nivel trófico inferior al propio. Para redes no ponderadas, esta información no está disponible por lo que el nivel trófico de redes no ponderadas se definía solo como basales, intermedias y topes (Cohen et al., 1990; Williams y Martinez, 2000). Las especies basales son aquellas que transforman la energía solar o elementos químicos en energía química y están relacionadas directamente con la productividad primaria, es decir las plantas, algas y diatomeas, por ejemplo (Arim y Marquet, 2004); por definición, estas especies no depredan a otras especies. Las especies intermedias son aquellas que depredan a las basales y también a otras especies intermedias (Alcorlo, 2004). Esta clase de especies también son depredadas por las especies tope. Como ejemplos tenemos a las aves, que se alimentan de semillas o plantas y también de insectos o lombrices. Por último, las especies ápice o tope son aquellas que se alimentan de otras especies, ya sean basales o intermedias, pero no son presa de alguna otra. Los ejemplos clásicos de especies tope serían los tiburones, la orca o los felinos como el jaguar. Williams y Martinez (2004) propusieron un algoritmo basado en la longitud de las cadenas tróficas capaz de calcular el nivel trófico de las especies muy cercano al obtenido cuando se conocen las proporciones de flujo de materia entre las especies en redes tróficas ponderadas.

Como puede deducirse, una red en general está formada por una gran cantidad de cadenas; estas cadenas están formadas por eslabones o nodos que representan las especies. La longitud de una cadena se puede medir contando el número de eslabones de un punto a otro, y en el caso de las cadenas tróficas, comenzando desde los productores primarios hasta una especie tope. Este es un aspecto de interés ecológico ya que, mientras más larga sea la cadena trófica, la transferencia de energía útil para cada nivel trófico disminuye considerablemente conforme avanzamos a los niveles tróficos superiores. En un principio, Lindeman (1942) propuso que la eficiencia de dicha transferencia es solo del 10% de una especie a la otra de niveles tróficos continuos. En varios estudios se ha demostrado que las cadenas tróficas largas no son energéticamente eficientes (Nielsen y Ulanowicz, 2000; Pimm, 1984; Pimm y Lawton, 1978) y, por lo tanto, las longitudes de las cadenas son cortas. Éste es uno de los aspectos del análisis de redes tróficas que continúa generando polémicas y estudios. ¿Por qué la longitud de las cadenas tróficas y, por lo mismo, el máximo nivel trófico, no sobrepasa el valor de 6? Varias teorías existen al respecto (Abdala-Roberts et al., 2019; Pringle, 2020; Massol et al., 2017; Post, 2002; Shanafelt y Loreau, 2018), pero además desde el punto de vista del manejo y la conservación, es importante el conocer en dónde se ubica nuestra especie objetivo con respecto al resto que forman el ecosistema.

Otras características estructurales han sido estudiadas utilizando métodos tomados de la sociología, de la informática y otros tipos de redes (Albert et al., 2000; Newman, 2003). Entre los aspectos estudiados destacan los valores de centralidad de las especies y la red en general (e.g., Abarca-Arenas et al., 2007; Cirtwill et al., 2018; Ibarra-García et al., 2020; Jordán, 2009; Jordán et al., 2007; Klesnikov et al., 2019; Rohr et al., 2016). Estos índices identifican la importancia de una especie con respecto al resto que componen la red.

Para calcular el valor de alguno de estos índices es necesario medir la longitud de las cadenas que conforman la red. Esto se hace contando el número de eslabones menos uno, en nuestro caso especies, que hay de uno a otro. Tomando como ejemplo la figura 1, existe una cadena que va desde la mantis hasta el halcón, la longitud de esta cadena es de 2, ya que, partiendo desde la mantis, pasa por el gorrión y finaliza en el halcón. Otro ejemplo, partiendo del pasto y terminado en la culebra podemos encontrar 2 cadenas. La primera está formada por pasto – ratón – culebra (longitud 2), la segunda es pasto – saltamontes – ratón – halcón – culebra (longitud 4). Conociendo estas cadenas y la posición dentro de ellas de las especies, se puede identificar el nivel de intermediarismo y cercanía de las especies entre sí, características que afectan al flujo de materia dentro de la red.

El nivel de intermediarismo de cada especie representa un papel importante dentro de la red ya que es un punto de enlace entre distintas especies para que la materia circule dentro del ecosistema (Newman, 2003). Una especie con un nivel de intermediarismo alto es la que interviene en la repartición de energía entre otras, además, si estas especies desaparecen, la red puede romperse afectando el flujo con la posibilidad de que algunas otras no puedan alimentarse. Otra métrica utilizada es la cercanía que proporciona un valor sobre qué tan cerca está una especie respecto a todas las demás (Opsahl et al., 2010). Ecológicamente, una especie cercana a otras implica que la materia está siendo transferida de manera más eficiente o rápida. Existen varios algoritmos que se aplican específicamente a redes dirigidas y pueden ser utilizados para el análisis de redes tróficas obteniendo resultados congruentes ecológicamente. Como ejemplo están los trabajos de Jordán (2009), Jordán et al. (2007) e Ibarra et al. (2020) en los que tratan de identificar las especies clave del ecosistema a través del análisis de las redes tróficas utilizando una metodología tomada del análisis de redes sociales (Cirtwill et al., 2018).

Finalmente, con el afán de reconstruir las redes tróficas, se han propuesto varios modelos que permiten simular éstas con distintos niveles de certeza. El primer modelo utilizado designa completamente al azar las presas del depredador, generalmente utilizando el modelo de Erdös-Rényi (Erdös y Rényi, 1959). No existe ningún tipo de restricción en este modelo y por ello los resultados con respecto a la estructura de la red simulada no corresponden a la red trófica observada, es decir, no tienen sentido ecológico por lo que generalmente no se utilizan. Sin embargo, una conclusión importante de estas discrepancias entre los modelos totalmente al azar y la red trófica real es que las redes tróficas presentan una estructura con cierto patrón determinado por las interacciones entre las especies y por lo tanto, éstas no son al azar.

Considerando el poco éxito del modelo totalmente al azar, Cohen et al. (1985) propusieron el modelo de cascada. Éste presenta una relación trófica entre las especies del ecosistema de una manera jerárquica, de tal forma que se genera una cascada de alimentación entre las especies basada en una jerarquía alimenticia. Los resultados del modelo fueron mejores que aquellos presentados por el modelo al azar, aunque varias características estructurales no pudieron ser representadas. Aunado a esto, el modelo se basó en redes tróficas muy pequeñas que no representaban de manera adecuada a los ecosistemas. Buscando mejores resultados, Williams y Martinez (2000) propusieron el modelo de nicho en el que las especies se alimentan de acuerdo con una distribución binomial y están arreglados a lo largo de un eje que representa el nicho alimenticio (Gallopin, 1989). Las variables bajo las cuales el modelo es ajustado son número de especies (S) y conectividad (C). El modelo de Williams y Martinez ha dado buenos resultados en la generación de redes tróficas similares a las observadas en la naturaleza (e.g., Camacho et al., 2007; Dunne y Williams, 2009; Stouffer et al., 2005; y muchas más). A partir de este modelo han surgido 2 variaciones, el modelo jerárquico anidado y el modelo general (Allesina et al., 2008; Cattin et al., 2004). El primero organiza a las especies a lo largo de un eje (nicho alimenticio) de acuerdo con una jerarquía dada por talla, biomasa e incluso taxonomía. El modelo general propone el uso de más de un eje de nicho para modelar las redes tróficas, siendo este modelo el que propone una mayor certidumbre (Allesina et al., 2008). Por último, Lafferty y Dunne (2010) propusieron el modelo SENO (por sus siglas en inglés, Stochastic Ecological Network Occupancy) en el que se calculan la probabilidad de interacción entre especies de acuerdo con el espacio y tiempo que comparten. Allhof et al. (2015) presentaron un modelo en el que se incorporó, además de las interacciones entre las especies, parámetros que simulan el crecimiento de las poblaciones involucradas y una tasa evolutiva de todas las especies. Los resultados del modelo son prometedores ya que se desvían muy poco de los parámetros estructurales de redes tróficas empíricas. 

Tabla 2

Ejemplo de una matriz de entrada – salida para ser utilizada en el estudio de redes tróficas ponderadas. Los números corresponden a g C m^-2 y^-1.

Matriz de interacción	Filtradores	Microbiota	Meiofauna	Alimentadores de deposito	Depredador	Detritus depositado	Entradas	Exportación	Respiración	Biomasa
Filtradores	0.0	0.0	0.0	0.0	0.5	15.8	41.5	25.2	0.0	0.0
Microbiota	0.0	0.0	1.2	1.2	0.0	0.0	0.0	5.8	0.0	0.0
Meiofauna	0.0	0.0	0.0	0.7	0.0	4.2	0.0	3.6	0.0	0.0
Alimentadores de depósito	0.0	0.0	0.0	0.0	0.2	1.9	0.0	0.4	0.0	0.0
Depredador	0.0	0.0	0.0	0.0	0.0	0.3	0.0	0.4	0.0	0.0
Detritus depositado	0.0	8.2	7.3	0.6	0.0	0.0	0.0	6.2	0.0	0.0

Redes tróficas ponderadas

Las redes ponderadas son aquellas donde se conoce la cantidad de materia transferida desde las presas hacia el depredador o desde las especies fuera del sistema hacia alguno de las especies dentro del sistema y viceversa. En este caso, la representación de las relaciones tróficas tiene una semejanza al sistema económico, en el que, en lugar de transferencia de dinero entre personas, existe la transferencia de materia entre especies. Leontief (1936) presentó un modelo llamado de entrada – salida para estudiar la economía de un país o ciudad, el modelo presenta la producción de distintos elementos de la economía de acuerdo con el flujo de dinero. A partir de este modelo, varios autores han propuesto su uso para medir la producción de una red trófica de acuerdo con la transferencia de materia entre las especies, generalmente en unidades de carbono por metro cuadrado por unidad de tiempo. Entre los principales exponentes de esta idea están Fath y Patten (1998), Patten (1978, 1985), Patten y Odum (1981), Polovina (1984), Ulanowicz (1986), Ulanowicz y Abarca-Arenas (1997), Ulanowicz y Puccia (1990), Ulanowicz y Norden (1990).

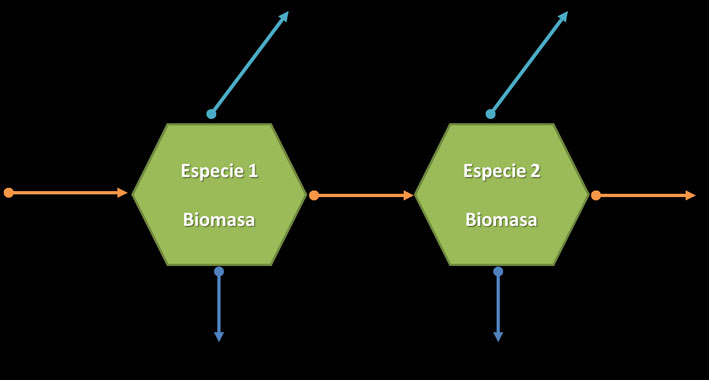
La tabla 2 muestra un ejemplo de los datos necesarios para un análisis de redes tróficas clásico. Comparando las tablas 1 y 2, la principal diferencia es que en la segunda se representan los flujos entre especies, en este caso g C m^-2 yr^-1. En principio, por razones termodinámicas, la cantidad de materia que entra al sistema debe ser igual a la cantidad que sale de la frontera del sistema y aquella que circula dentro del mismo, el sistema debe estar balanceado. Considerando esto, la matriz de transferencias de materia está formada por las especies del sistema en la que se denota la cantidad de materia (biomasa) utilizada de las presas (renglones) por los depredadores (columnas). Además de este flujo, pueden existir flujos que entran al sistema desde fuera de sus fronteras y también flujos que salen del mismo. Las primeras son las entradas (inputs) y los segundos la exportación (outputs). En lo que respecta a las especies, éstas tienen los siguientes flujos: entradas desde fuera del sistema (importación), salida del sistema (exportación), flujo de una especie hacia otra (depredación) y pérdidas por respiración (fig. 3). Hemos mencionado que el sistema de flujos debe estar balanceado, esto se puede comprobar cuando la suma de los renglones de una matriz como la de la tabla 2 es igual a la suma de las columnas.

Métodos de análisis

Una vez balanceado el sistema, Ulanowicz (1986) propuso una serie de índices que muestran el estado de desarrollo y crecimiento del ecosistema, estos índices están basados en la teoría de la información (Ulanowicz, 1986; Ulanowicz y Abarca-Arenas, 1997; Ulanowicz y Norden, 1990). De esta forma, a partir de la entropía condicional y la información mutua promedio, se propone el índice ascendencia, que está relacionado con el desarrollo y el crecimiento de un ecosistema (Ulanowicz, 1986). Podríamos decir que este índice mide la diversidad del ecosistema en términos de sus flujos de materia. La ecuación para medir la ascendencia es (Ulanowicz y Norden, 1990): 

Donde Tij es la cantidad de materia que va del nodo i al nodo j, es la suma de todos los flujos y

que es la suma del renglón i y columna j, respectivamente.

Este valor de ascendencia tiene un límite superior llamado capacidad y la diferencia entre esta capacidad y la ascendencia es el llamado gasto no utilizado. Ulanowicz y Abarca-Arenas (1997) expandieron el análisis de la ascendencia al considerar las biomasas de los componentes del ecosistema; de esta forma es posible medir las variaciones de flujos y biomasas como parte de las interacciones de las especies y su entorno. Como un ejemplo del uso de los varios índices podemos mencionar a Ulanowicz y Baird (1999), que hicieron una comparación de la dinámica de flujos de carbono, nitrógeno y fósforo de la comunidad de la bahía de Chesapeake utilizando estos índices. Otros trabajos son los de Jordán y Scheuring (2004), Kluger et al. (2016), Lau et al. (2017), Nogues et al. (2021), Scharler et al. (2015), Smit (2021), Tomczak et al. (2013) y Yin et al. (2021).

Uno de los efectos más claros de la relación depredador-presa es que cuando el depredador aumenta la tasa de consumo de la presa, ésta disminuye su biomasa. Sin embargo, el decremento de la biomasa de la presa ocasiona un incremento en la biomasa del alimento de la presa, de tal forma que, de manera indirecta, el primer depredador beneficia a la presa de su presa (Abrams et al., 1996; Zhao et al., 2016). Estos efectos son importantes para entender la estructura y dinámica de la red trófica y se pueden dar a distintas distancias de los depredadores. Por ejemplo, supongamos que existe una especie bajo explotación y se propone realizar un plan de manejo de dicho recurso. La primera aproximación sería determinar las tasas de crecimiento y mortalidades natural y por explotación y tamaño de la población de la especie sujeta a explotación.

Con base en esos datos, se simulan distintos escenarios de explotación y se determinan las políticas de extracción del recurso de acuerdo con la ganancia o pérdida de biomasa. Sin embargo, es muy posible que estas políticas traigan consigo a mediano y largo plazo consecuencias no previstas sobre el propio recurso objetivo y el resto del ecosistema al desestimar el efecto sobre otras especies directa e indirectamente (Nogues et al., 2021; Tomczac et al., 2013; Zhao et al., 2016). Conociendo las relaciones indirectas que el recurso objetivo genera con el resto de las especies del ecosistema, nos daríamos cuenta de las repercusiones que las políticas de extracción pudieran tener sobre la estructura y dinámica del sistema. Con esta información, el manejo del recurso se tendría que expandir a más especies y no solo a la especie objetivo para no vulnerar la salud del ecosistema. 

Utilizando los datos de una red trófica ponderada también es posible determinar el nivel de resiliencia del ecosistema después de una perturbación, es decir, el tiempo necesario para que el ecosistema regrese a su estado anterior a una perturbación. Esto se puede realizar simulando la disminución de biomasa de una o más especies a lo largo del tiempo y determinar el tiempo necesario para que el sistema regrese (o no) a su estado anterior a la perturbación. Es importante destacar que la disminución de biomasas implica necesariamente un decremento en las tasas de flujo de materia entre las especies. Un ejemplo de este tema es el trabajo publicado por Arreguín-Sánchez (2014), en el que muestra un método para medir el nivel de resiliencia del ecosistema a través del uso de modelos tróficos. Concluyendo que la resiliencia del ecosistema depende del nivel de estrés al que fue sometido.

Como en el caso de las redes no ponderadas, la gran mayoría de las redes tróficas analizadas hasta el momento representan una fotografía del momento dentro de un espacio determinado; ésto es, los datos para construirla son el producto de un promedio de varios muestreos a lo largo de un tiempo determinado en el espacio. Ésto representa un problema dentro de la escala temporal ya que es muy probable que una red trófica construida a través de la ponderación anual de datos sea diferente a una que represente una temporada del año o un ciclo de 24 horas (Abarca-Arenas et al., 2007). Un ejemplo de la importancia de análisis trófico en el tiempo es el trabajo de Ibarra-García et al. (2020), en el que muestran la evolución de un arrecife coralino antes y después de ser expuesto a un huracán. En sus resultados se observa cómo la red trófica cambia, pero después de unos años la estructura de ésta tiende a regresar a su estado anterior al huracán. Para el caso del espacio o área que circunscribe el ecosistema en estudio, las redes tróficas también están delimitadas y existen pocas aproximaciones sobre el efecto que tiene el tamaño del área y la estructura de las redes tróficas. Sobre ésto, Brose et al. (2004) aproximaron la relación especies – área y número de interacciones – área, para obtener un modelo que disminuya en cierta medida el nivel de incertidumbre. Esta aproximación tiene la ventaja de que no solo estudia el flujo de especies dentro de un área, sino que también la interacción entre distintos sistemas a través del flujo de materia y no solo de biomasas (migraciones). 

Comentarios finales

Como hemos visto, el análisis de las redes tróficas, en cualquiera de sus modalidades, es una herramienta muy poderosa para el estudio de muchas de las características de un ecosistema. A partir de estudios ecosistémicos utilizando las redes tróficas ha sido posible y lo será más aún en el futuro, identificar patrones del comportamiento de sus propiedades a lo largo de variables como tiempo y espacio. Este será un gran paso hacia adelante en la constante búsqueda de la ley ecológica que tanto pretenden algunos investigadores.

La biodiversidad no solo es el número de especies y sus abundancias en un espacio y tiempo determinados, también implica la interacción entre estas especies. Las interacciones son de todos los tipos posibles, por ejemplo, depredador – presa, parasitismo, mutualismo y éstas son el resultado de millones de años de evolución y coevolución. A través de estudios paleontológicos se ha demostrado que la estructura y función de antiguos ecosistemas era muy similar a la actual, algo así como la misma película, pero con diferentes actores. Este es un tema importante e interesante para el estudio de la biodiversidad utilizando las redes tróficas. El conocimiento del pasado nos ayudará a entender el futuro de los ecosistemas actuales y cómo conservarlos y manejarlos de la mejor manera posible, sin alterar aspectos clave de éste. Para lograr esto es necesario conocer los patrones de estructura de distintos tipos de sistemas naturales, a diferentes latitudes, y considerando distintas escalas espaciales y temporales.

Los parásitos abundan en todos los ecosistemas, algunos más nocivos que otros, sin embargo, el papel que juegan en el intricado flujo de energía dentro de un ecosistema es todavía confuso. Determinar cómo intervienen los parásitos en el flujo de materia ayudaría a entender la evolución de éstos, así como la de sus hospederos. Desde el punto de vista dinámico, las redes tróficas en las que se involucran los parásitos nos ayudarían a completar algunas lagunas respecto a la función general de los ecosistemas. Conocer el papel que juegan los parásitos facilitaría el entendimiento de los ciclos de materia en los que intervienen y así identificar los puntos clave para su control. Siendo parte del ecosistema ¿qué efectos tienen los parásitos sobre la biodiversidad al afectar niveles tróficos superiores? sería una pregunta por contestar.

Procesos como el ciclo del agua, fertilización de suelos y microclimas son dependientes de la biodiversidad, así como el alimento humano. Los servicios que un ecosistema otorga al ser humano como son agua, alimento y recreación dependen directamente de la biodiversidad y ésta implica la interacción entre las especies que integran ese ecosistema. Esas interacciones son el tema central de las redes tróficas. Al estudiar las redes tróficas podemos generar escenarios para conocer el efecto de la eliminación de especies sobre la estructura y función del sistema o la implantación de especies exóticas sobre los valores de biomasa de especies que se utilizan como alimento humano. 

Agradecimientos

A la Dirección General de Investigaciones de la Universidad Veracruzana por el apoyo brindado para el desarrollo de este escrito. 

Referencias

Abarca-Arenas, L. G., Franco-Lopez, J., Peterson, M. S., Brown-Peterson, N. J. y Valero-Pacheco, E. (2007). Sociometric analysis of the role of penaeids in the continental shelf food web off Veracruz, Mexico based on by-catch. Fisheries Research, 87, 46–57. https://doi.org/10.1016/j.fishres.2007.06.019 

Abarca-Arenas, L. G. y Ulanowicz, R. E. (2002). The effects of taxonomic aggregation on network analysis. Ecological Modelling, 149, 285–296. https://doi.org/10.1016/S0304-3800(01)00474-4 

Abdala-Roberts, L., Puentes, A., Finke, D. L., Marquis, R. J., Montserrat, M., Poelman, E. H. (2019). Tri-trophic interactions: Bridging species, communities and ecosystems. Ecology Letters, 22, 2151–2167. https://doi.org/10.1111/ele.13392 

Abrams, P. A., Menge, B. A., Mittelbach, G. G., Spiller, D. A. y Yodzis, P. (1996). The role of indirect effects in food webs. En G. A. Polis y K. O. Winemiller (Eds.), Food webs (pp. 371–395). Boston, MA: Springer US. https://doi.org/10.1007/978-1-4615-7007-3_36 

Albert, R., Jeong, H. y Barabási, A. L. (2000). Error and attack tolerance of complex networks. Nature, 406, 378–382. https://doi.org/10.1038/35019019 

Alcorlo, P. (2004). Las redes tróficas en las lagunas salinas temporales de Los Monegros (Zaragoza, España). Ecosistemas, 13, 37–51.

Allesina, S., Alonso, D., & Pascual, M. (2008). A general model for food web structure. Science, 320, 658–661. https://doi.org/10.1126/science.1156269 

Allhoff, K. T., Ritterskamp, D., Rall, B. C., Drossel, B. y Guill, C. (2015). Evolutionary food web model based on body masses gives realistic networks with permanent species turnover. Scientific Reports, 5, 10955. https://doi.org/10.1038/srep10955 

Arim, M. y Marquet, P. A. (2004). Intraguild predation: a widespread interaction related to species biology: intraguild predation. Ecology Letters, 7, 557–564. https://doi.org/10.1111/j.1461-0248.2004.00613.x 

Arreguín-Sánchez, F. (2014). Measuring resilience in aquatic trophic networks from supply-demand-of-energy relationships. Ecological Modelling, 272, 271–276. https://doi.org/10.1016/j.ecolmodel.2013.10.018 

Barabási, A. L. (2002). Linked: the new science of networks. Cambridge, MA: Perseus Publishing.

Borgatti, S. P., Mehra, A., Brass, D. J. y Labianca, G. (2009). Network analysis in the Social Sciences. Science, 323, 892–895. https://doi.org/10.1126/science.1165821 

Brose, U., Ostling, A., Harrison, K. y Martinez, N. D. (2004). Unified spatial scaling of species and their trophic interactions. Nature, 428, 167–171. https://doi.org/10.1038/nature02297 

Camacho, J., Stouffer, D. B. y Amaral, L. A. N. (2007). Quantitative analysis of the local structure of food webs. Journal of Theoretical Biology, 246, 260–268. https://doi.org/10.1016/j.jtbi.2006.12.036 

Cattin, M. F., Bersier, L. F., Banašek-Richter, C., Baltensperger, R. y Gabriel, J. P. (2004). Phylogenetic constraints and adaptation explain food-web structure. Nature, 427, 835–839. https://doi.org/10.1038/nature02327 

Cirtwill, A. R., Dalla-Riva, G. V., Gaiarsa, M. P., Bimler, M. D., Cagua, E. F., Coux, C. et al. (2018). A review of species role concepts in food webs. Food Webs, 16, e00093. https://doi.org/10.1016/j.fooweb.2018.e00093 

Cohen, J. E. (1978). Food webs and niche space. Princeton, NJ: Princeton University Press. https://doi.org/10.2307/j.ctvx5wc04 

Cohen, J. E., Briand, F. y Newman, C. M. (1990). Community food webs: data and theory. Berlin: Springer-Verlag. https://doi.org/10.1007/978-3-642-83784-5 

Cohen, J. E., Jonsson, T. y Carpenter, S. R. (2003). Ecological community description using the food web, species abundance, and body size. Proceedings of the National Academy of Sciences, 100, 1781–1786. https://doi.org/10.1073/pnas.232715699

Cohen, J. E., Newman, C. M. y Steele, J. H. (1985). A stochastic theory of community food webs I. Models and aggregated data. Proceedings of the Royal Society of London, 224, 421–448. https://doi.org/10.1098/rspb.1985.0042 

DeAngelis, D. L. y Gross, L. J. (Eds.). (2018). Individual-based models and approaches in ecology: populations, communities, and ecosystems. New York: Chapman and Hall.

Digel, C., Curtsdotter, A., Riede, J., Klarner, B. y Brose, U. (2014). Unravelling the complex structure of forest soil food webs: higher omnivory and more trophic levels. Oikos, 123, 1157–1172. https://doi.org/10.1111/oik.00865 

Dunne, J. A. y Williams, R. J. (2009). Cascading extinctions and community collapse in model food webs. Philosophical Transactions of the Royal Society B, 364, 1711–1723. https://doi.org/10.1098/rstb.2008.0219 

Dunne, J. A., Williams, R. J. y Martínez, N. D. (2002). Food-web structure and network theory: The role of connectance and size. Proceedings of the National Academy of Sciences, 99, 12917–12922. https://doi.org/10.1073/pnas.192407699 

Erdös, P. y Rényi, A. (1959). On random graphs I. Publicationes Mathematicae Debrecen, 6, 290–297.

Fath, B. D. y Patten, B. C. (1998). Network synergism: Emergence of positive relations in ecological systems. Ecological Modelling, 107, 127–143. https://doi.org/10.1016/S0304-3800(97)00213-5

Fox-Keller, E. (2007). A clash of two cultures. Nature, 445, 603–603. https://doi.org/10.1038/445603a 

Gallopín, G. C. (1989). A unified concept of the ecological niche. International Journal of General Systems, 15, 59–73. https://doi.org/10.1080/03081078908935030 

Hall, S. J. y Raffaelli, D. (1991). Food-web patterns: lessons from a species-rich web. Journal of Animal Ecology, 60, 823–841.

Ibarra-García, E. C., Abarca-Arenas, L. G., Ortiz, M. y Rodríguez-Zaragoza, F. A. (2020). Impact of hurricane Dean on Chinchorro Bank coral reef (Western Caribbean): Temporal variation in the food web structure. Ecological Indicators, 118, 106712. https://doi.org/10.1016/j.ecolind.2020.106712 

Ings, T. C., Montoya, J. M., Bascompte, J., Blüthgen, N., Brown, L., Dormann, C. F. et al. (2009). Ecological networks —beyond food webs. The Journal of Animal Ecology, 78, 253–269. https://doi.org/10.1111/j.1365-2656.2008.01460.x 

Jordán, F. (2009). Keystone species and food webs. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 364, 1733–1741. https://doi.org/10.1098/rstb.2008.0335 

Jordán, F., Benedek, Z. y Podani, J. (2007). Quantifying positional importance in food webs: a comparison of centrality indices. Ecological Modelling, 205, 270–275. https://doi.org/10.1016/j.ecolmodel.2007.02.032 

Jordán, F. y Scheuring, I. (2004). Network ecology: topological constraints on ecosystem dynamics. Physics of Life Reviews, 1, 139–172. https://doi.org/10.1016/j.plrev.2004.08.001 

Kluger, L. C., Taylor, M. H., Mendo, J., Tam, J. y Wolff, M. (2016). Carrying capacity simulations as a tool for ecosystem-based management of a scallop aquaculture system. Ecological Modelling, 331, 44–55. https://doi.org/10.1016/j.ecolmodel.2015.09.002 

Koehn, L. E., Essington, T. E., Marshall, K. N., Kaplan, I. C., Sydeman, W. J., Szoboszlai, A. I. et al. (2016). Developing a high taxonomic resolution food web model to assess the functional role of forage fish in the California current ecosystem. Ecological Modelling, 335, 87–100. https://doi.org/10.1016/j.ecolmodel.2016.05.010 

Kolesnikov, V., Anikin, V., Mosolova, E., Faizliev, A., Mironov, S., Zemlyanskaya, M. et al. (2019). Food Chain Analysis Based on Graph Centrality Indicators. Journal of Physics: Conference Series, 1334, 012004. https://doi.org/10.1088/1742-6596/1334/1/012004

Lafferty, K. D. y Dunne, J. A. (2010). Stochastic ecological network occupancy (SENO) models: A new tool for modeling ecological networks across spatial scales. Theoretical Ecology, 3, 123–135. https://doi.org/10.1007/s12080-010-0082-0 

Lau, M. K., Borrett, S. R., Baiser, B., Gotelli, N. J. y Ellison, A. M. (2017). Ecological network metrics: Opportunities for synthesis. Ecosphere, 8, e01900. https://doi.org/10.1002/ecs2.1900 

Leontief, W. W. (1936). Quantitative input and output relations in the economic systems of the United States. The Review of Economics and Statistics, 18, 105–125. https://doi.org/10.2307/1927837 

Lindeman, R. L. (1942). The trophic-dynamic aspect of ecology. Bulletin of Mathematical Biology, 53, 167–191. 

Martinez, N. D. (1991). Artifacts or attributes? Effects of resolution on the Little Rock Lake food web. Ecological Monographs, 61, 367–392. https://doi.org/10.2307/2937047 

Martinez, N. D. (1992). Constant connectance in community food webs. The American Naturalist, 139, 1208–1218.

Martinez, N. D. (1993). Effects of resolution on food web structure. Oikos, 66, 403–412. https://doi.org/10.2307/3544934 

Massol, F., Dubart, M., Calcagno, V., Cazelles, K., Jacquet, C., Kéfi, S. et al. (2017). Island biogeography of food webs. En D. A. Bohan, A. J. Dumbrell, y F. Massol (Eds.), Advances in ecological research. Vol. 56 (pp. 183–262). London: Academic Press. https://doi.org/10.1016/bs.aecr.2016.10.004 

May, R. M. (1972). Will a large complex system be stable? Nature, 238, 413–414. https://doi.org/10.1038/238413a0 

May, R. M. (1974). Stability and complexity in model ecosystems. Princeton: Princeton University Press. https://doi.org/10.2307/j.ctvs32rq4 

Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Review, 45, 167–256. https://doi.org/10.1137/s003614450342480 

Nielsen, S. N. y Ulanowicz, R. E. (2000). On the consistency between thermodynamical and network approaches to ecosystems. Ecological Modelling, 132, 23–31. https://doi.org/10.1016/S0304-3800(00)00302-1 

Nogues, Q., Raoux, A., Araignous, E., Chaalali, A., Hattab, T., Leroy, B. et al. (2021). Cumulative effects of marine renewable energy and climate change on ecosystem properties: Sensitivity of ecological network analysis. Ecological Indicators, 121, 107128. https://doi.org/10.1016/j.ecolind.2020.107128 

Ocampo-Reinaldo, M., Milessi, A. C., Romero, M. A., Crespo, E., Wolff, M. y González, R. A. (2016). Assessing the effects of demersal fishing and conservation strategies of marine mammals over a Patagonian food web. Ecopath 30 years – Modelling ecosystem dynamics: beyond boundaries with EwE. Ecological Modelling, 331, 31–43. https://doi.org/10.1016/j.ecolmodel.2015.10.025 

Olivier, P. y Planque, B. (2017). Complexity and structural properties of food webs in the Barents Sea. Oikos, 126, 1339–1346. https://doi.org/10.1111/oik.04138 

Opsahl, T., Agneessens, F. y Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks, 32, 245–251. https://doi.org/10.1016/j.socnet.2010.03.006 

Patonai, K. y Jordán, F. (2017). Aggregation of incomplete food web data may help to suggest sampling strategies. Ecological Modelling, 352, 77–89. https://doi.org/10.1016/j.ecolmodel.2017.02.024

Patten, B. C. (1978). Systems approach to the concept of environment. The Ohio Journal of Science, 78, 206–222.

Patten, B. C. (1985). Energy cycling in the ecosystem. Ecological Modelling, 28, 1–71. https://doi.org/10.1016/0304-3800(85)90013-4 

Patten, B. C. y Odum, E. P. (1981). The cybernetic nature of ecosystems. The American Naturalist, 118, 886–895. https://doi.org/10.1086/283881 

Pimm, S. L. (1979). The structure of food webs. Theoretical Population Biology, 16, 144–158. https://doi.org/10.1016/0040-5809(79)90010-8 

Pimm, S. L. (1982). Food webs. New York: Chapman and Hall.

Pimm, S. L. y Lawton, J. H. (1978). On feeding on more than one trophic level. Nature, 275, 542–544. https://doi.org/10.1038/275542a0 

Polovina, J. J. (1984). Model of a coral reef ecosystem. Coral Reefs, 3, 1–11. https://doi.org/10.1007/BF00306135 

Post, D. M. (2002). The long and short of food-chain length. Trends in Ecology & Evolution, 17, 269–277. https://doi.org/10.1016/S0169-5347(02)02455-2 

Pringle, R. M. (2020). Untangling food webs. En A. Dobson, D. Tilman y R. D. Holt (Eds.), Unsolved problems in Ecology (pp. 225–238). Princeton: Princeton University Press. https://doi.org/doi:10.1515/9780691195322-020 

Riede, J. O., Rall, B. C., Banasek-Richter, C., Navarrete, S. A., Wieters, E. A., Emmerson, M. C. et al. (2010). Chapter 3— Scaling of food-web properties with diversity and complexity across ecosystems. En G. Woodward (Ed.), Advances in ecological research. Vol. 42 (pp. 139–170).
London: Academic Press. https://doi.org/10.1016/B978-0-12-381363-3.00003-4 

Rohr, R. P., Naisbit, R. E., Mazza, C. y Bersier, L. F. (2016). Matching–centrality decomposition and the forecasting of new links in networks. Proceedings of the Royal Society B, 283, 20152702. https://doi.org/10.1098/rspb.2015.2702

Roopnarine, P. D., Angielczyk, K. D., Wang, S. C. y Hertog, R. (2007). Trophic network models explain instability of Early Triassic terrestrial communities. Proceedings of the Royal Society B, 274, 2077–2086. https://doi.org/10.1098/rspb.2007.0515 

Scharler, U. M., Ulanowicz, R. E., Fogel, M. L., Wooller, M. J., Jacobson-Meyers, M. E., Lovelock, C. E. et al. (2015). Variable nutrient stoichiometry (carbon:nitrogen: phosphorus) across trophic levels determines community and ecosystem properties in an oligotrophic mangrove system. Oecologia, 179, 863–876. https://doi.org/10.1007/s00442-015-3379-2 

Shanafelt, D. W. y Loreau, M. (2018). Stability trophic cascades in food chains. Royal Society Open Science, 5, 180995. https://doi.org/10.1098/rsos.180995 

Sinclair, A. R. E., Pech, R. P., Dickman, C. R., Hik, D., Mahon, P. y Newsome, A. E. (1998). Predicting effects of predation on conservation of endangered prey. Conservation Biology, 12, 564–575.

Smit, K. P., Bernard, A. T. F., Lombard, A. T. y Sink, K. J. (2021). Assessing marine ecosystem condition: A review to support indicator choice and framework development. Ecological Indicators, 121, 107148. https://doi.org/10.1016/j.ecolind.2020.107148 

Stouffer, D. B., Camacho, J., Guimerà, R., Ng, C. A. y Nunes Amaral, L. A. (2005). Quantitative patterns in the structure of model and empirical food webs. Ecology, 86, 1301–1311.

Sugihara, G., Bersier, L. F. y Schoenly, K. (1997). Effects of taxonomic and trophic aggregation on food web properties. Oecologia, 112, 272–284.

Sugihara, G., Schoenly, K. y Trombla, A. (1989). Scale invariance in food web properties. Science, 245, 48–52. https://doi.org/10.1126/science.2740915 

Tomczak, M. T., Heymans, J. J., Yletyinen, J., Niiranen, S., Otto, S. A. y Blenckner, T. (2013). Ecological Network Indicators of Ecosystem Status and Change in the Baltic Sea. Plos One, 8, e75439. https://doi.org/10.1371/journal.pone.0075439 

Trifonova, N., Kenny, A., Maxwell, D., Duplisea, D., Fernandes, J. y Tucker, A. (2015). Spatio-temporal Bayesian network models with latent variables for revealing trophic dynamics and functional networks in fisheries ecology. Ecological Informatics, 30, 142–158. https://doi.org/10.1016/j.ecoinf.2015.10.003 

Turney, S. y Buddle, C. M. (2016). Pyramids of species richness: the determinants and distribution of species diversity across trophic levels. Oikos, 125, 1224–1232. https://doi.org/10.1111/oik.03404 

Ulanowicz, R. E. (1986). Growth and development: ecosystems phenomenology. New York: Springer.

Ulanowicz, R. E. (2009). The dual nature of ecosystem dynamics. Ecological Modelling, 220, 1886–1892. https://doi.org/10.1016/j.ecolmodel.2009.04.015 

Ulanowicz, R. E. y Abarca-Arenas, L. G. (1997). An informational synthesis of ecosystem structure and function. Ecological Modelling, 95, 1–10. https://doi.org/10.1016/S0304-3800(96)00032-4 

Ulanowicz, R. E. y Baird, D. (1999). Nutrient controls on ecosystem dynamics: The Chesapeake mesohaline community. Journal of Marine Systems, 19, 159–172.
https://doi.org/10.1016/S0924-7963(98)90017-3 

Ulanowicz, R. E. y Norden, J. S. (1990). Symmetrical overhead in flow networks. International Journal of Systems Science, 21, 429–437. https://doi.org/10.1080/00207729008910372 

Ulanowicz, R. E. y Puccia, C. J. (1990). Mixed trophic impacts ecosystems. Coenoses, 5, 7–16.

Vermaat, J. E., Dunne, J. A. y Gilbert, A. J. (2009). Major dimensions in food-web structure properties. Ecology, 90, 278–282. https://doi.org/10.1890/07-0978.1

Wasserman, S. y Faust, K. (1994). Social network analysis: methods and applications. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511815478 

Williams, R. J. y Martinez, N. D. (2000). Simple rules yield complex food webs. Nature, 404, 180–183. https://doi.org/10.1038/35004572 

Williams, R. J. y Martinez, N. D. (2004). Limits to trophic levels and omnivory in complex food webs: theory and data. The American Naturalist, 163, 458–468. https://doi.org/10.1086/381964 

Yen, J. D. L., Cabral, R. B., Cantor, M., Hatton, I., Kortsch, S., Patrício, J. et al. (2016). Linking structure and function in food webs: maximization of different ecological functions generates distinct food web structures. Journal of Animal Ecology, 85, 537–547. https://doi.org/10.1111/1365-2656.12484 

Yin, J., Xu, J., Xue, Y., Xu, B., Zhang, C., Li, Y. et al. (2021). Evaluating the impacts of El Niño events on a marine bay ecosystem based on selected ecological network indicators. Science of The Total Environment, 763, 144205. https://doi.org/10.1016/j.scitotenv.2020.144205 

Zhao, L., Zhang, H., O’Gorman, E. J., Tian, W., Ma, A., Moore, J. C. et al. (2016). Weighting and indirect effects identify keystone species in food webs. Ecology Letters, 19, 1032–1040. https://doi.org/10.1111/ele.12638